Tìm số tự nhiên x biết rằng 3 số 15;35 và x tích của 2 số nao cũng chia hết cho số còn lại
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Điều kiện: \(x\ge74\)
\(GT\Rightarrow\left\{{}\begin{matrix}x+15=m^2\left(m\in N\right)\\x-74=n^2\left(n\in N\right)\end{matrix}\right.\)
\(\Rightarrow m^2-15=n^2+74\)
\(\Leftrightarrow m^2-n^2=89\Leftrightarrow\left(m+n\right)\left(m-n\right)=89\)
Do \(m,n\in N\) và \(89=1\cdot89\) nên ta có:
Trường hợp 1: \(\left\{{}\begin{matrix}m+n=1\\m-n=89\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=45\\n=-44\end{matrix}\right.\) (loại).
Trường hợp 2: \(\left\{{}\begin{matrix}m+n=89\\m-n=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=45\\n=44\end{matrix}\right.\) (nhận).
\(\Rightarrow x=m^2-15=45^2-15=2010\left(TM\right)\)
Vậy: \(x=2010\).

Bài 1:
a: Ta có: \(48751-\left(10425+y\right)=3828:12\)
\(\Leftrightarrow y+10425=48751-319=48432\)
hay y=38007
b: Ta có: \(\left(2367-y\right)-\left(2^{10}-7\right)=15^2-20\)
\(\Leftrightarrow2367-y=1222\)
hay y=1145
Bài 2:
Ta có: \(8\cdot6+288:\left(x-3\right)^2=50\)
\(\Leftrightarrow288:\left(x-3\right)^2=2\)
\(\Leftrightarrow\left(x-3\right)^2=144\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=12\\x-3=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=15\\x=-9\end{matrix}\right.\)

126 ⋮ x; 210 ⋮ x => x ∈ UC(126,210)
ƯCLN(126,210) = 42
ƯC(126,42) = Ư(42) = {1;2;3;6;7;14;21;42}
Vì 15 < x < 30 nên x = 21

Vì 126 ⋮ x và 210 ⋮ x nên x ∈ ƯC(126; 210)
Ta có: 126 = 2.32.7
210 = 2.3.5.7
ƯCLN(126;210) = 2.3.7 = 42
ƯC(126;210) = {1;2;3;6;7;14;21;42}
Vì 15 < x < 30 nên x = 21
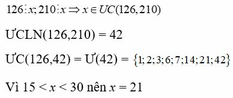
Vì tích của 2 số nào cũng chia hết cho các số còn lại nên tích của 15 và 35 chia hết cho x.
\(15.35⋮x\)\(\Rightarrow525⋮x\Leftrightarrow x\inƯ\left(525\right)\)
Bằng phép thử trực tiếp ta thấy x=21 thỏa mãn đề bài.
Thử lại:\(15.21=315⋮35\)
\(21.35=735⋮15\)
\(15.35=525⋮21\)
Vậy x là 21 là số tự nhiên cần tìm.