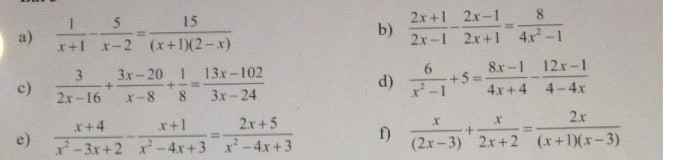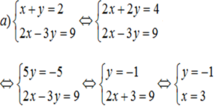K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
HS
Hương sullky
29 tháng 1 2017 - olm
Câu 1: giải các phương trình ;a, x.(2x-9)=3x.(x-5)             b,(2x-1)^2-(2x+1)^2=4.(x-3)                c,2x+3/3+3x+2/2=2,5x-1                  d,2-x/2001-1=1-x/2002-x/2003e, x+1/3+3.(2x+1)/4=2x+3.(x+1)/6+7+12x/12Câu 2:giải các phương trình sau:a,(x^2-6x+9)^2-15(x^2-6x+10)=1        b,(x^2+1)+3x(x^2+1)+2x^2=0                  c,(x^2-9)^2=12x+1              d,x63=3x62=4x=2=0              e,x^4+x^2+6x-8=0          g, (x^2-4x)2+(x-2)62=10                      ...
Đọc tiếp

Câu 1: giải các phương trình ;

a, x.(2x-9)=3x.(x-5)             b,(2x-1)^2-(2x+1)^2=4.(x-3)                c,2x+3/3+3x+2/2=2,5x-1                  d,2-x/2001-1=1-x/2002-x/2003

e, x+1/3+3.(2x+1)/4=2x+3.(x+1)/6+7+12x/12

Câu 2:giải các phương trình sau:

a,(x^2-6x+9)^2-15(x^2-6x+10)=1        b,(x^2+1)+3x(x^2+1)+2x^2=0                  c,(x^2-9)^2=12x+1              d,x63=3x62=4x=2=0              e,x^4+x^2+6x-8=0          g, (x^2-4x)2+(x-2)62=10                       h,(12x+7)(3x+2)(2x+1)=3                i,(x^2+5x+4)(9x^2+30x+16)=4x^2        k, (x^2+x+1)^2=3(x^4+x^2+1)                       l, 6x^4+25x^3+12x^2-25x+6=0
#Toán lớp 8
0
MT
Ma Tiến Khôi
4 tháng 5 2022
câu 1 giải các phương trình sau.a) 4x+8=3x-15b) \(\dfrac{x+2}{x-2}-\dfrac{1}{x}=\dfrac{2}{x\left(x-2\right)}\)câu 2 giải các bất phương trình sau và biểu diễn tập nghiệm trên trục sốa) 2x-8\(\ge\)0.b)10+10x>0câu 3 giải bài toán bằng các lập phương trìnhMột học sinh đi từ nhà đến trường với vận tốc 15km/h,rồi từ trường về nhà với vận tốc 20km/h.Biết thời gian đi nhiều hơn thời gian về là 15 phút. Tĩnh quãng đường...
Đọc tiếp

câu 1 giải các phương trình sau.

a) 4x+8=3x-15

b) \(\dfrac{x+2}{x-2}-\dfrac{1}{x}=\dfrac{2}{x\left(x-2\right)}\)

câu 2 giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số

a) 2x-8\(\ge\)0.

b)10+10x>0

câu 3 giải bài toán bằng các lập phương trình

Một học sinh đi từ nhà đến trường với vận tốc 15km/h,rồi từ trường về nhà với vận tốc 20km/h.Biết thời gian đi nhiều hơn thời gian về là 15 phút. Tĩnh quãng đường từ nhà đến trường của người đó.

câu 4 Cho hình chữ nhật ABCD có AB=8cm,BC=6cm.Kẻ đường cao AH của tam giác ADB(AH\(\perp\)DB,H\(\in\)DB).

a) Chúng minh \(\Delta\)HAD đồng dạng \(\Delta\)ABD.

b) Chứng minh:AD\(^2\)=DH.DB.

c)Tính độ dài các đoạn thẳng AH,DH.

d) Tính tỉ số diện tích \(\Delta\)HAD và \(\Delta\)ABD từ đó suy ra tỉ số đồng dạng của nó.

         giúp mình với mai mình thi rồi SOS !!!!!!!

 

 
#Toán lớp 8
1
NL
Nguyễn Lê Phước Thịnh
18 tháng 6 2023

2:

a: =>x-4>=0

=>x>=4

b: =>x+1>0

=>x>-1

Đúng(0)
NT
Nguyễn thị Phụng
19 tháng 1 2021
           ĐỀ THI HỌC KỲ I  Câu 1 : giải phương trình ln (3x2 - 2x +1) = ln ( 4x - 1) Câu 2 : Tìm tập hợp các giá trị của tham số m để phương trình 3x + 3 = m \(\sqrt{9^x+1}\) có đúng 1 nghiệm Câu 3 : Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = -x3 + 3mx + 1 có 2 điểm cực trị A , B sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ...
Đọc tiếp

           ĐỀ THI HỌC KỲ I  

Câu 1 : giải phương trình ln (3x2 - 2x +1) = ln ( 4x - 1) 

Câu 2 : Tìm tập hợp các giá trị của tham số m để phương trình 3x + 3 = m \(\sqrt{9^x+1}\) có đúng 1 nghiệm 

Câu 3 : Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = -x3 + 3mx + 1 có 2 điểm cực trị A , B sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ ) 

 
#Toán lớp 12
0
TL
Thao Ly Nguyen
18 tháng 3 2022
Câu 1:  Giải các phương trình sau:a)      3- 4x (25 - 2x ) = 8x2 + x - 300b)       c)     ...
Đọc tiếp

Câu 1:  Giải các phương trình sau:

a)      3- 4x (25 - 2x ) = 8x2 + x - 300

b)       

c)       

 
#Toán lớp 8
1
Q
qlamm
18 tháng 3 2022

câu bc hình bị lỗi

Đúng(0)
TT
Trọng tâm Nguyễn
14 tháng 1 2022

1) Cho phương trình 2 - 2mx-m – 2=0(1), với ta là tham số. a) Giải phương trình (L) khi m=2 b) Tìm các giá trị của đế phương trình (1) có hai nghiêm X1X2 sao cho biểu thức có trị lớn nhất MÌNH CẦN CÂU B THÔI Ạ ( CÂU B ĐỪNG DÙNG VI-ET)😅
#Toán lớp 9
0
NT
Nguyễn Thị Quỳnh Như
29 tháng 5 2021
Câu 1: Rút gọn biểu thức sau: A = \(\left(\sqrt{3}+1\right)\sqrt{\dfrac{14-6\sqrt{3}}{5+\sqrt{3}}}\)Câu 2: 2.1 Giải các phương trình sau a/ x2 = (x-1)(3x-2)b/ 9x4+5x2-4= 02.2 Giải bài toán sau bằng cách lập phương trình: một đội xe cần chở 120 tấn hàng, hôm làm việc có 2 xe bị điều đi nơi khác nên mỗi xe phải,chở thêm 3 tấn nữa. Tính số xe lúc đầu của độiBài 3: Cho parabol (P): y= ax2 và đường thẳng (d): y= mx+ 1a) Tìm a biết (P)...
Đọc tiếp

Câu 1: Rút gọn biểu thức sau: A = \(\left(\sqrt{3}+1\right)\sqrt{\dfrac{14-6\sqrt{3}}{5+\sqrt{3}}}\)

Câu 2: 

2.1 Giải các phương trình sau 

a/ x2 = (x-1)(3x-2)

b/ 9x4+5x2-4= 0

2.2 Giải bài toán sau bằng cách lập phương trình: một đội xe cần chở 120 tấn hàng, hôm làm việc có 2 xe bị điều đi nơi khác nên mỗi xe phải,chở thêm 3 tấn nữa. Tính số xe lúc đầu của đội

Bài 3: Cho parabol (P): y= ax2 và đường thẳng (d): y= mx+ 1

a) Tìm a biết (P) đi qua điểm A (2;-4). Vẽ (P) với a tìm được 

b) Tìm giá trị của m để đường thẳng (d) tiếp xúc với parabol (P). Tìm tọa độ tiếp điểm 

Bài 4: Cho phương trình: x2 -(2m -1)x + m2 -1 = 0, m là tham số 

a) Tìm các giá trị của m để phương trình có 2 nghiệm phân biệt 

b) Gọi X1x2 lần lượt là hai nghiệm của phương trình. Tìm m để phương trình có hai nghiệm thỏa mản: (x1 -x2)2 = x1 -3x2

Bài 5: Cho đường tròn (O;R) và một điểm nằm ngoài đường tròn. Từ A kẻ 2 tiếp tuyến AB,AC và một cát tuyến AMN đến O

a. Chứng minh: AB2 = AM.AN 

b/ Gọi i là trung điểm MN,Ci cắt đường tròn tại K. Chứng minh A, B, i, O 

cùng thuộc một đường tròn và BK//MN

c) gọi H là giao điểm của AO và BC. Chứng minh tứ giác HMNO nội tiếp và HB là phân giác của góc MHN

 
#Toán lớp 9
4
AT
An Thy
29 tháng 5 2021

1.\(A=\left(\sqrt{3}+1\right)\sqrt{\dfrac{14-6\sqrt{3}}{5+\sqrt{3}}}=\left(\sqrt{3}+1\right)\sqrt{\dfrac{\left(14-6\sqrt{3}\right)\left(5-\sqrt{3}\right)}{\left(5+\sqrt{3}\right)\left(5-\sqrt{3}\right)}}\)

\(=\left(\sqrt{3}+1\right)\sqrt{\dfrac{44\left(2-\sqrt{3}\right)}{22}}=\left(\sqrt{3}+1\right)\sqrt{4-2\sqrt{3}}=\left(\sqrt{3}+1\right)\sqrt{\left(\sqrt{3}-1\right)^2}\)

\(=\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)=2\)

Đúng(1)
AT
An Thy
29 tháng 5 2021

2.1.a) \(x^2=\left(x-1\right)\left(3x-2\right)\Leftrightarrow x^2=3x^2-5x+2\Leftrightarrow2x^2-5x+2=0\)

\(\Leftrightarrow\left(x-2\right)\left(2x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{2}\end{matrix}\right.\)

b) \(9x^4+5x^2-4=0\Leftrightarrow9x^4+9x^2-4x^2-4=0\)

\(\Leftrightarrow9x^2\left(x^2+1\right)-4\left(x^2+1\right)=0\Leftrightarrow\left(x^2+1\right)\left(9x^2-4\right)=0\)

mà \(x^2+1>0\Rightarrow9x^2=4\Rightarrow x^2=\dfrac{4}{9}\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)

2) Gọi số xe lúc đầu của đội là a(xe) \(\left(a\in N,a>0\right)\)

Theo đề,ta có: \(\left(a-2\right)\left(\dfrac{120}{a}+3\right)=120\Leftrightarrow120+3a-\dfrac{240}{a}-6=120\)

\(\Leftrightarrow\dfrac{3a^2-6a-240}{a}=0\Rightarrow3a^2-6a-240=0\Rightarrow a^2-2a-80=0\)

\(\Leftrightarrow\left(a+8\right)\left(a-10\right)=0\) mà \(a>0\Rightarrow a=10\)

 

Đúng(1)
CN
Chí Nguyễn
25 tháng 4 2023

Câu 2 . Cho phương trình: x’ – 2(m-1)x – 2m+1=0 (m là tham số). a) Giải phương trình với m=4 b) Tìm các giá trị của m để phương trình có hai nghiệm x và y thỏa mãn 2x, +3x=-11 cứu tuii:((
#Toán lớp 9
1
NL
Nguyễn Lê Phước Thịnh
25 tháng 4 2023

a: Khi m=4 thì (1) sẽ là:

x^2-6x-7=0

=>x=7 hoặc x=-1

b: Sửa đề: 2x1+3x2=-11

x1+x2=2m-2

=>2x1+3x2=-11 và 2x1+2x2=4m-4

=>x2=-11-4m+4=-4m-7 và x1=2m-2+4m+7=6m+5

x1*x2=-2m+1

=>-24m^2-20m-42m-35+2m-1=0

=>-24m^2-60m-34=0

=>\(m=\dfrac{-15\pm\sqrt{21}}{12}\)

Đúng(1)
BU
Black Undo
20 tháng 3 2022
a)Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn ? x – 2=0;            ;             ;2x2 + 3 = 0          ;     4– 0,2x = 0          b)Hãy giải các phương trình bậc nhất một ẩn có ở câu a)...
Đọc tiếp

a)Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn ?

 x – 2=0;            ;             ;2x2 + 3 = 0          ;     4– 0,2x = 0

          b)Hãy giải các phương trình bậc nhất một ẩn có ở câu a) ?
#Toán lớp 8
1
QN
Quảng Nguyễn
20 tháng 3 2022

a) PT bậc nhất một ẩn là: x-2=0; 4-0,2x=0
b) Giải:
x-2=0     (*)
⟺ x=-2
Vậy tập nghiệm của pt (*) là S={-2}
 4-0,2x=0    (**)
⟺-0,2x=-4
⟺x=-4/-0,2=20
Vậy tập nghiệm của pt (**) là S={20}

Đúng(0)
G
Giang シ)
16 tháng 3 2022
Câu 2:  Giải các hệ phương trình...
Đọc tiếp

Câu 2:  Giải các hệ phương trình sau:

a. \left\{\begin{array}{l}\mathrm{x}+2 \mathrm{y}=5 \\ 3 \mathrm{x}+4 \mathrm{y}=5\end{array}\right.

b. \left\{\begin{array}{l}3 x+y=3 \\ 2 x-y=7\end{array}\right.
#Toán lớp 9
2
VD
Vô danh
16 tháng 3 2022

\(a,\left\{{}\begin{matrix}x+2y=5\\3x+4y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=5-2y\\3\left(5-2y\right)+4y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=5-2y\\15-6y+4y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=5-2y\\15-2y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=5-2.5\\y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=5\end{matrix}\right.\)

\(b,\left\{{}\begin{matrix}3x+y=3\\2x-y=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3-3x\\2y-\left(3-3x\right)=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3-3x\\2y-3+3x=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3-3x\\5x-3=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3-3.2\\x=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)

Đúng(2)
G
Giang シ)
16 tháng 3 2022

mik c.ơn 

Đúng(0)
TL
Tuyết Ly
22 tháng 4 2022

Giải các phương trình sau: giải giúp mình câu c; d với ạ

undefined
#Toán lớp 8
1
NL
Nguyễn Lê Phước Thịnh
25 tháng 6 2023

c: ĐKXĐ: x<>8

\(\dfrac{3}{2x-16}+\dfrac{3x-20}{x-8}+\dfrac{1}{8}=\dfrac{13x-102}{3x-24}\)

=>\(\dfrac{9}{6\left(x-8\right)}+\dfrac{18x-120}{6\left(x-8\right)}-\dfrac{26x-204}{6\left(x-8\right)}=\dfrac{-1}{8}\)

=>\(\dfrac{18x-111-26x+204}{6\left(x-8\right)}=\dfrac{-1}{8}\)

=>\(\dfrac{-8x+93}{6x-48}=\dfrac{-1}{8}\)

=>\(\dfrac{8x-93}{6x-48}=\dfrac{1}{8}\)

=>8(8x-93)=6x-48

=>64x-744-6x+48=0

=>58x=696

=>x=12

d: ĐKXĐ: x<>1; x<>-1

\(\dfrac{6}{x^2-1}+5=\dfrac{8x-1}{4x+4}+\dfrac{12x-1}{4x-4}\)

=>\(\dfrac{24}{4\left(x-1\right)\left(x+1\right)}+\dfrac{20\left(x^2-1\right)}{4\left(x-1\right)\left(x+1\right)}=\dfrac{\left(8x-1\right)\left(x-1\right)+\left(12x-1\right)\left(x+1\right)}{4\left(x-1\right)\left(x+1\right)}\)

=>8x^2-9x+1+12x^2+12x-x-1=24+20x^2-20

=>20x^2+2x=20x^2+4

=>2x=4

=>x=2(loại)

Đúng(0)
PT
Pham Trong Bach
24 tháng 10 2019

Phần tự luận

Nôi dung câu hỏi 1

Giải các hệ phương trình sau

a)  x + y = 2 2 x - 3 y = 9

#Toán lớp 9
1
CM
Cao Minh Tâm
24 tháng 10 2019

Vậy hệ phương trình có nghiệm duy nhất là (x; y) = (3; -1)

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP