Cho 3x4-4x2-4 = 4y4+10y2-x2y2. Chứng minh x2-y2 = 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(x^4+2x^3-4x-4=\left(x^4+2x^3+x^2\right)-\left(x^2+4x+4\right)\)
\(=\left(x^2+x\right)^2-\left(x+2\right)^2=\left(x^2+x-x-2\right)\left(x^2+x+x+2\right)\)
\(=\left(x^2-2\right)\left(x^2+2x+2\right)\)
a) Ta có: \(x^4+2x^3-4x-4\)
\(=\left(x^4+2x^3+x^2\right)-\left(x^2+4x+4\right)\)
\(=\left(x^2+x\right)^2-\left(x+2\right)^2\)
\(=\left(x^2+x-x-2\right)\left(x^2+x+x+2\right)\)
\(=\left(x^2-2\right)\cdot\left(x^2+2x+2\right)\)

1:
=x^2-6x+9-4=(x-3)^2-4>=-4
Dấu = xảy ra khi x=3
3: =-y^2-4y-4+13
=-(y+2)^2+13<=13
Dấu = xảy ra khi y=-2
4: D=x^2-8>=-8
Dấu = xảy ra khi x=0

9: \(\left(-2x\right)\left(3x^2-2x+4\right)=-6x^3+4x^2-8x\)

a: \(x^2+4x+4=x^2+2\cdot x\cdot2+2^2=\left(x+2\right)^2\)
b: \(4x^2-4x+1=\left(2x\right)^2-2\cdot2x\cdot1+1^2=\left(2x-1\right)^2\)
c: \(2x-1-x^2\)
\(=-\left(x^2-2x+1\right)=-\left(x-1\right)^2\)
d: \(x^2+x+\dfrac{1}{4}=x^2+2\cdot x\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2=\left(x+\dfrac{1}{2}\right)^2\)
e: \(9-x^2=3^2-x^2=\left(3-x\right)\left(3+x\right)\)
g: \(\left(x+5\right)^2-4x^2=\left(x+5+2x\right)\left(x+5-2x\right)\)
\(=\left(5-x\right)\left(5+3x\right)\)
h: \(\left(x+1\right)^2-\left(2x-1\right)^2\)
\(=\left(x+1+2x-1\right)\left(x+1-2x+1\right)\)
\(=3x\left(-x+2\right)\)
i: \(=x^2y^2-4xy+4-3\)
\(=\left(xy-2\right)^2-3=\left(xy-2-\sqrt{3}\right)\left(xy-2+\sqrt{3}\right)\)
k: \(=y^2-\left(x-1\right)^2\)
\(=\left(y-x+1\right)\left(y+x-1\right)\)
l: \(=x^3+3\cdot x^2\cdot2+3\cdot x\cdot2^2+2^3=\left(x+2\right)^3\)
m: \(=\left(2x\right)^3-3\cdot\left(2x\right)^2\cdot y+3\cdot2x\cdot y^2-y^3=\left(2x-y\right)^3\)

Với x, y là hai số dương, dễ dàng chứng minh x + y 2,
do x + y = 2 => 0 < xy ≤ 1 (1)
Ta lại có: 2xy( x2 + y2) ≤
=> 0 < 2xy(x2 + y2) ≤ (x+y)4/4 = 4
=> 0 < xy( x2 + y2) ≤ 2 (2)
Nhân (1) với (2) theo vế ta có: x2y2 ( x2 + y2) ≤ 2 (đpcm)
Dấu “=” xảy ra khi x = y = 1

e: \(x^2+6x+9-y^2\)
\(=\left(x+3\right)^2-y^2\)
\(=\left(x+3-y\right)\left(x+3+y\right)\)
f: \(x^2-2x+7x-14\)
\(=x\left(x-2\right)+7\left(x-2\right)\)
=(x-2)(x+7)
h: \(5x^2-10xy+5y^2-20\)
\(=5\left(x^2-2xy+y^2-4\right)\)
\(=5\left(x-y-2\right)\left(x-y+2\right)\)

a: \(3x^4-6x^3+2x^2=x^2\left(3x^2-6x+2\right)\)
b: \(x^3y+12x^2y+36xy=xy\left(x^2+12x+36\right)=xy\left(x+6\right)^2\)
c: \(x^3y-9xy^3=xy\left(x^2-9y^2\right)=xy\left(x-3y\right)\left(x+3y\right)\)
d: \(x^2y^2-2xy^2+y^2=y^2\left(x-1\right)^2\)

\(=\left(x^2+y^2-2xy\right)\left(x^2+y^2+2xy\right)\)
\(=\left(x+y\right)^2\cdot\left(x-y\right)^2\)

\(=\left(x^2+y^2-5\right)^2-4\left(xy+2\right)^2\\ =\left(x^2+y^2-5-2xy-4\right)\left(x^2+y^2-5+2xy+4\right)\\ =\left[\left(x-y\right)^2-9\right]\left[\left(x+y\right)^2-1\right]\\ =\left(x-y-3\right)\left(x-y+3\right)\left(x+y-1\right)\left(x+y+1\right)\)
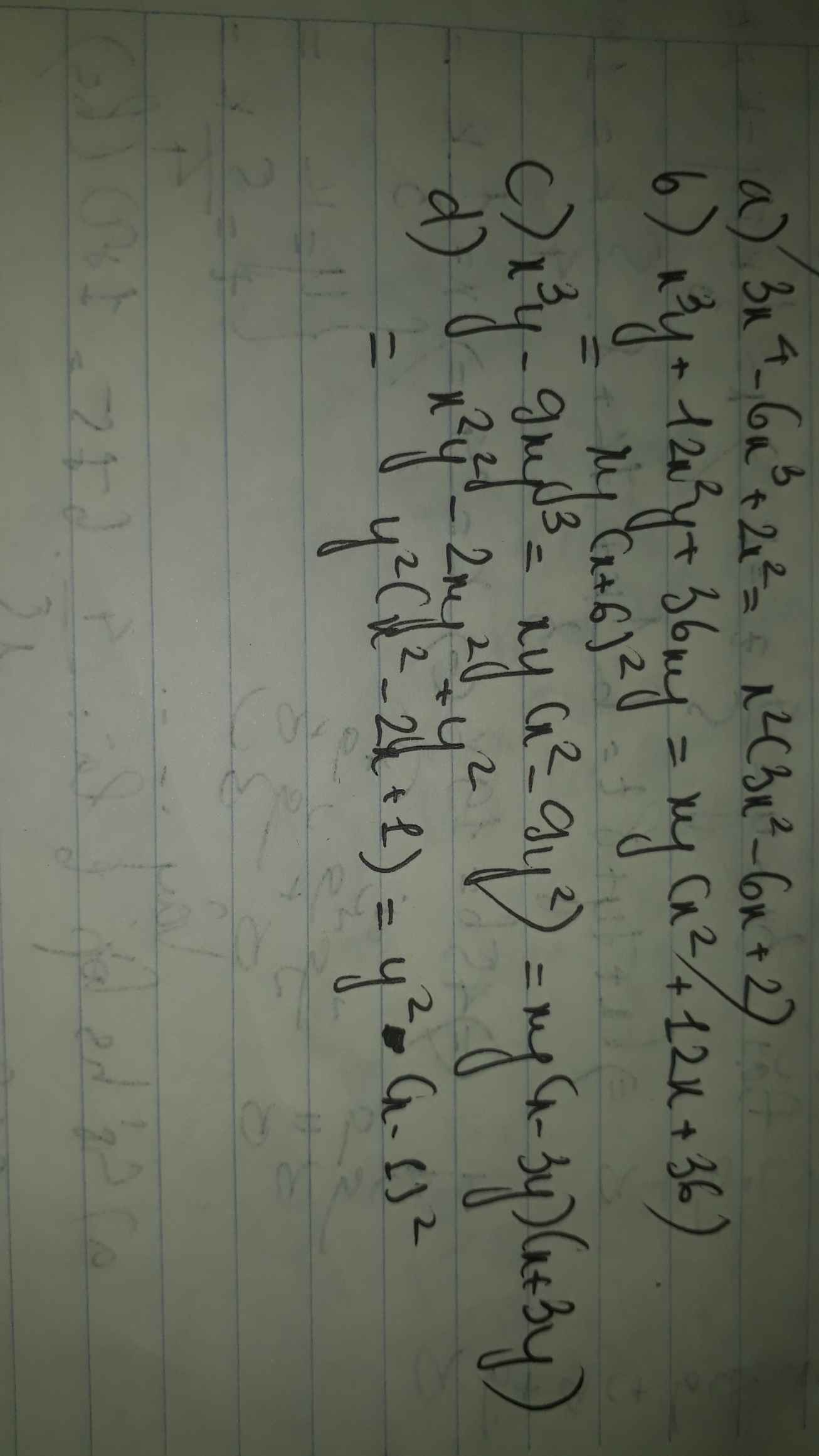
Lời giải:
$3x^4-4x^2-4=4y^4+10y^2-x^2y^2$
$\Leftrightarrow 3x^4-4x^2-4-4y^4-10y^2+x^2y^2=0$
$\Leftrightarrow 3x^2(x^2-y^2-2)+4y^2(x^2-y^2-2)+2(x^2-y^2-2)=0$
$\Leftrightarrow (x^2-y^2-2)(3x^2+4y^2+2)=0$
$\Leftrightarrow x^2-y^2-2=0$ (do $3x^2+4y^2+2>0$)
$\Leftrightarrow x^2-y^2=2$