Thực hiện tương tự như Hoạt động 1 với các dãy số từ 0 đến 15 để tìm mã hóa của các số từ 8 đến 15 và đưa ra nhận xét.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Dũng
CTVVIP
25 tháng 10 2023
Sử dụng hệ cơ số 2 (hệ nhị phân)
Ta có:
Số 3 trong hệ nhị phân là 0011.
Số 6 trong hệ nhị phân là 0110.
Vậy số 3 được mã hóa thành dãy "0011" và số 6 được mã hóa thành dãy "0110" trong hệ nhị phân.
LN
3 tháng 11 2023
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
lần 1 0 1 2 3 4 5 6 7 | trái 0
lần 2 0 1 2 3|trái 0
lần 3 | 2 3 phải 1
lần 4 | 3 phải 1
3=0011
mã hóa số 6 :
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
lần 1 :0 1 2 3 4 5 6 7 | trái 0
lần 2: | 4 5 6 7 phải 1
lần 3: | 6 7 phải 1
lần 4: 6 | trái 0
6=0110
GX
1
ND
1
ND
1
15 tháng 11 2022
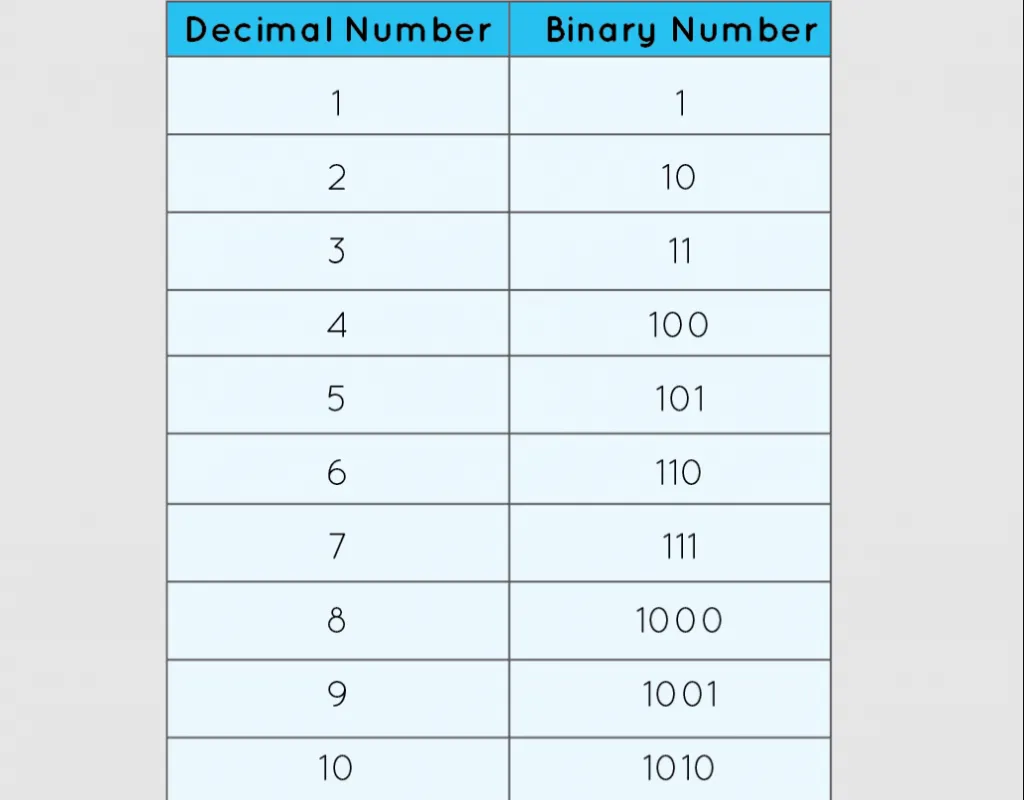
- 8 = 23 = 1000.
- 9 = 23 + 1 = 1001.
- 10 = 23 + 2 = 23 + 21 = 1010.
- 11 = 23 + 21 + 1 = 1011.
- 12 = 23 + 22 = 1100.
- 13 = 23 + 22 + 1 = 1101.
- 14 = 23 + 22 + 21 = 1110.
- 15 = 23 + 22 + 21 + 20 (20 = 1) = 1111.
14 tháng 11 2021
0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15
/10,11,12,13,14,15 phải
10,11,12/trái
10,11/12 trái
10/12trái
mã hóa số 10 = 1 0 0 0
14 tháng 11 2021
\(0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15\)
\(|10,11,12,13,14,15\) \(phải\) \(1\)
\(10,11,12\) \(|\) \(trái\)\(0\)
\(10,11|\) \(trái\) \(0\)
\(10|\) \(trái\) \(0\)
\(\Rightarrow10=1000\)
Để mã hóa một số, làm tương tự như hoạt động 1, ta cần phải thực hiện 4 lần thu gọn dãy số từ 0 đến 15. Kết quả thu được:
⇒ Nhận xét: Mã hóa của các số từ 8 đến 15 khác nhau.