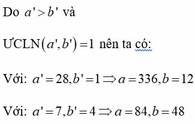tìm a,b dương biết a+b; a-b; ab tỉ lệ nghịch với 35; 210; 12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GD
1
27 tháng 1 2023
\(\dfrac{a+b+a}{b}=38-a-b\)
\(\dfrac{a}{b}+\dfrac{b}{b}+\dfrac{a}{b}=38-a-b\)
\(\dfrac{2a}{b}+1=38-a-b\)
\(\left(\dfrac{2a}{b}+1\right)-1=\left(38-a-b\right)-1\)
\(\dfrac{2a}{b}=37-a-b\)
\(\dfrac{a}{b}=\dfrac{37-a-b}{2}\)
(Bài toán rất phức tạp, dừng như đây không phải của lớp 7!)
\(\left\{{}\begin{matrix}a=0;b=37\\a=12;b=1\\a=12;b=24\end{matrix}\right.\) và \(\left\{{}\begin{matrix}a=-38;b=1\\a=-38;b=76\end{matrix}\right.\)
PT
1
PT
1
CM
29 tháng 3 2017
Ta có: a.b = BCNN(a,b).ƯCLN(a,b) = 336.12 = 4032.
Vì ƯCLN(a,b) = 12 => a = 12a’, b = 12b’ (a’, b’N), ƯCLN(a’,b’) = 1
=>12a’.12b’ = 4032 => a’b’ = 4032:(12.12) = 28
Do a’ > b’ và ƯCLN(a’,b’) = 1 nên ta có:
Với: a’ = 28, b’ = 1 => a = 336 ; b = 12.
Với: a’ = 7, b = 4 => a = 84, b = 48
PT
1
CM
11 tháng 9 2018
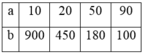
Vì (a,b) = 10 nên a = 10x, b = 10y, với (x,y)=1
Suy ra a.b=10x.10y = 100xy.
Lại có a.b = [a,b].(a,b) = 900.10 = 9000
Suy ra 100xy = 9000 => xy = 90
Giả sử x<y và (x,y)=1 ta có các trường hợp sau:
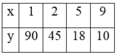
Từ đó suy ra a,b có các trường hợp sau:
PT
1
