một phân số có tổng tử và mẫu là 15 nếu giảm tử đi 5 đơn vị và tăng mẫu thêm 2 đơn vị thì được phân số mới bằng 1/5 tìm phân số ban đầu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 5 2020
Gọi tử số là x
Mẫu số là 15 - x
Theo đề ra, ta có phương trình:
\(\frac{x-5}{15-x+2}=\frac{1}{5}\)
\(\Leftrightarrow\frac{x-5}{17-x}=\frac{1}{5}\)
\(\Leftrightarrow5\left(x-5\right)=17-x\)
\(\Leftrightarrow5x-25=17-x\)
\(\Leftrightarrow5x+x=17+25\)
\(\Leftrightarrow6x=42\)
\(\Leftrightarrow x=7\)
Vậy tử số là 7, mẫu số là 15 - 7 = 8 => Phân số ban đầu là \(\frac{7}{8}\)
CM
18 tháng 12 2017
Gọi tử số của phân số ban đầu là a, theo bài ra ta có:
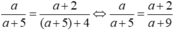
(Điều kiện: a ≠ - 5;a ≠ - 9 )
a(a + 9) = (a + 2)(a + 5)
⇔ a 2 + 9 a = a 2 + 7 a + 10
⇔ 2a = 10 ⇔ a = 5 (Thỏa mãn)
Vậy phân số cần tìm là: 5/10
H9
HT.Phong (9A5)
CTVHS
4 tháng 5 2023
Gọi z là tử của phân số
Khi đó mẫu của phân số là \(z-13\)
Phân số ta cần tìm có dạng: \(\dfrac{z}{z-13}\)
Nếu tăng tử lên 3 đơn vị và giảm mẫu đi 4 đơn vị thì được phân số bằng với phân số \(\dfrac{3}{5}\) nên ta có phương trình:
\(\dfrac{z+3}{z-13-4}=\dfrac{3}{5}\left(z\ne17\right)\)
\(\Leftrightarrow\dfrac{z+3}{z-17}=\dfrac{3}{5}\)
\(\Leftrightarrow\dfrac{5\left(z+3\right)}{5\left(z-17\right)}=\dfrac{3\left(z-17\right)}{5\left(z-17\right)}\)
\(\Leftrightarrow5z+15=3z-51\)
\(\Leftrightarrow5z-3z=-51-15\)
\(\Leftrightarrow2z=-66\)
\(\Leftrightarrow z=\dfrac{-66}{2}=-33\left(tm\right)\)
Vậy phân số ta cần tìm là: \(\dfrac{z}{z-13}=\dfrac{-33}{-33-13}=\dfrac{-33}{-46}=\dfrac{33}{46}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
4 tháng 5 2023
Hiệu số phần bằng nhau:
5-3=2(phần)
Nếu tăng tử số 3 đơn vị, giảm mẫu số 4 đơn vị được phân số mơi có mẫu số bẻ hơn tử số:
13 + (4+3)= 20 (đơn vị)
Tử số mới là:
20:2 x3=30
Tử số ban đầu là:
30-3=27
Mẫu số ban đầu là:
27-13=14
Phân số ban đầu là: 27/14
6 tháng 5 2021
Gọi tử số là x
Mẫu số là: x+8
Theo đề bài ta có:
\(\frac{x+2}{x+8-3}=\frac{3}{4}\)
\(\Leftrightarrow\frac{x+2}{x+5}=\frac{3}{4}\)
\(\Leftrightarrow3\cdot\left(x+5\right)=4\cdot\left(x+2\right)\)
\(\Leftrightarrow3x+15=4x+8\)
\(\Leftrightarrow-x=-7\)
\(\Leftrightarrow x=7\)
Suy ra: tử số là 7
Mẫu số là: 7+8 = 15
Vậy phân số cần tìm là: \(\frac{7}{15}\)
4 tháng 5 2019
Gọi tử số của phân số ban đầu là x
Mẫu số của phân số ban đầu là x+13
Tử số của phân số mới là x+3
Mẫu số của phân số mới là x+13-4= x+9
Phân số mới là \(\frac{x+3}{x+9}\)
Theo bài ra ta có phương trình
\(\frac{x+3}{x+9}\)= \(\frac{3}{5}\)
bạn tự giả phương trình nhé thì sẽ được x=6
=> tử số của phân số ban đầu là 6
Mẫu số của phân số ban đầu là 6+13=19
Vậy phân số ban đầu là \(\frac{6}{19}\)
PJ
31 tháng 5 2016
Gọi từ số của phân số cần tìm là: a.
Gọi mẫu số của phân số cần tìm là:b
Theo đề ta có:
\(a=b-8\)
\(\Rightarrow\frac{a}{b}=\frac{a}{a+8}\)
Ta lại có:
\(\frac{a+3}{a+8-3}=\frac{5}{6}\)\(\Rightarrow\frac{a+3}{a+5}=\frac{5}{6}\)
\(\Rightarrow\frac{a+5-2}{a+5}=\frac{5}{6}\Rightarrow\frac{a+5}{a+5}-\frac{2}{a+5}=\frac{5}{6}\)
\(=1-\frac{2}{a+5}=\frac{5}{6}\)
\(\frac{2}{a+5}=1-\frac{5}{6}=\frac{1}{6}\)
\(a+5=\frac{2}{\frac{1}{6}}=12\)
\(a=12-5=7\)
\(=>b=7+8=15\)
Vậy phân số ban đầu là: \(\frac{7}{15}\)
21 tháng 12 2020
Gọi tử số là x.( ĐK: x thuộc Z)
=> Mẫu số là x + 3
=> Phân số ban đầu là: x/x + 3
Khi tăng cả tử và mẫu của nó thêm 2 đơn vị thì được phân số mới là:
x + 2/x + 5
=> Ta có phương trình:
x+2/x+5 = 1/2 (ĐKXĐ: x + 5 ≠ 0 <=> x ≠ -5)
<=> 2(x + 2) = x + 5
⇔ 2x + 4 = x + 5
⇔ x = 1
Vậy phân số ban đầu là : 1/4
Đáp án là ⅞
bạn giải ra giúp mình được không ạ ?