Cho đường tròn (O) đường kính AB, kẻ 2 đường thẳng d1;d2 lần lượt vuông góc với AB tại A,B. Trên đường thẳng d1 lấy C bất kì (C≠A) đường vuông góc với CO tại O cắt d2 tại điểm O
a, Xét vị trí tương đối của đường thẳng CD với đường tròn (O)
b, Xđ vị trí điểm C để AC+BD nhỏ nhất
c,Giả sử AB=2a.Tính AC.BD theo a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 8 2023
a: Xét (OC/2) có
góc OMC là góc nội tiếp chắn nửa đường tròn
=>góc OMC=90 độ
=>CM vuông góc MO
Xét (O') có
góc BPC nội tiếp
BC là đường kính
=>góc BPC=90 độ
=>BP vuông góc CM
=>BP//OM
7 tháng 12 2023
a: Ta có: \(\widehat{CHB}=90^0\)
=>ΔCHB vuông tại H
=>ΔCHB nội tiếp đường tròn đường kính CB(4)
Ta có: \(\widehat{CKB}=90^0\)
=>ΔCKB vuông tại K
=>ΔCKB nội tiếp đường tròn đường kính CB(5)
Từ (4) và (5) suy ra C,H,B,K cùng thuộc đường tròn đường kính CB
b:
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Ta có: \(\widehat{OCB}+\widehat{BCK}=\widehat{OCK}=90^0\)
\(\widehat{OCB}+\widehat{OCA}=\widehat{BCA}=90^0\)
Do đó: \(\widehat{BCK}=\widehat{OCA}\)(1)
Ta có: CHBK là tứ giác nội tiếp
=>\(\widehat{BCK}=\widehat{BHK}\left(2\right)\)
Xét ΔOAC có OC=OA
nên ΔOAC cân tại O
=>\(\widehat{OAC}=\widehat{OCA}\)(3)
Từ (1),(2),(3) suy ra \(\widehat{BHK}=\widehat{OAC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên HK//AC
7 tháng 12 2023
Xét tứ giác CHBK có
\(\widehat{CHB}+\widehat{CKB}=90^0+90^0=180^0\)
=>CHBK là tứ giác nội tiếp
=>C,H,B,K cùng thuộc một đường tròn
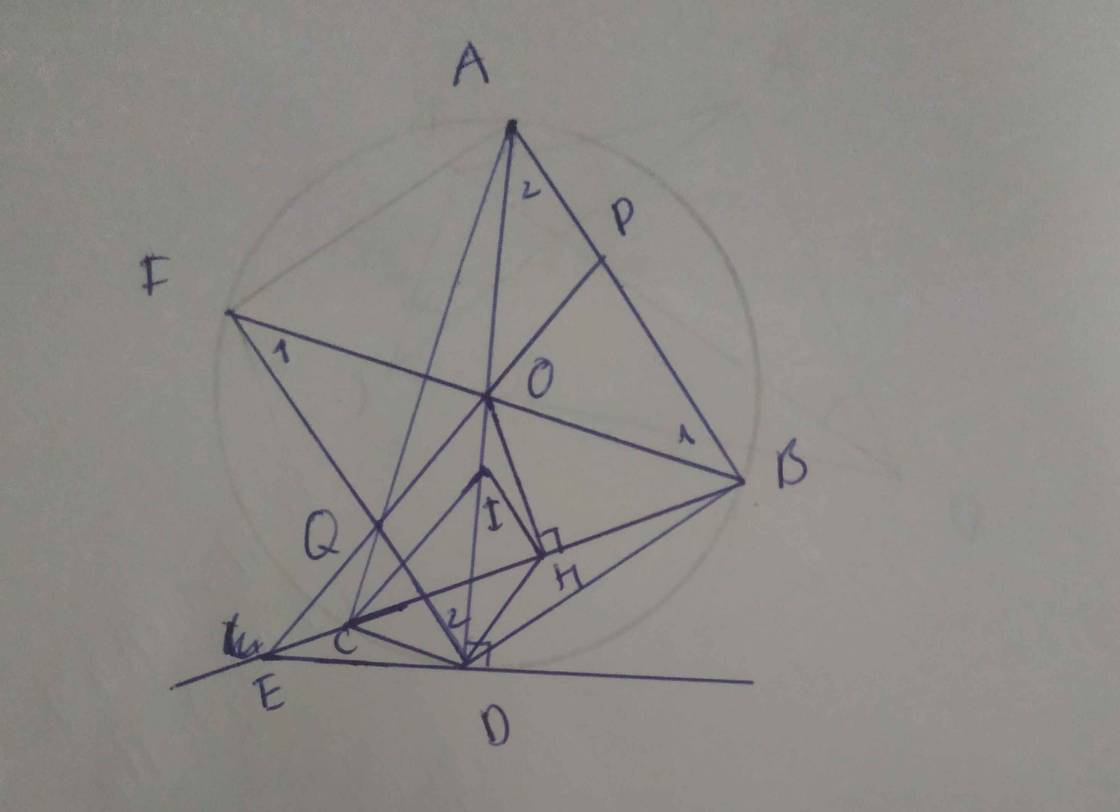
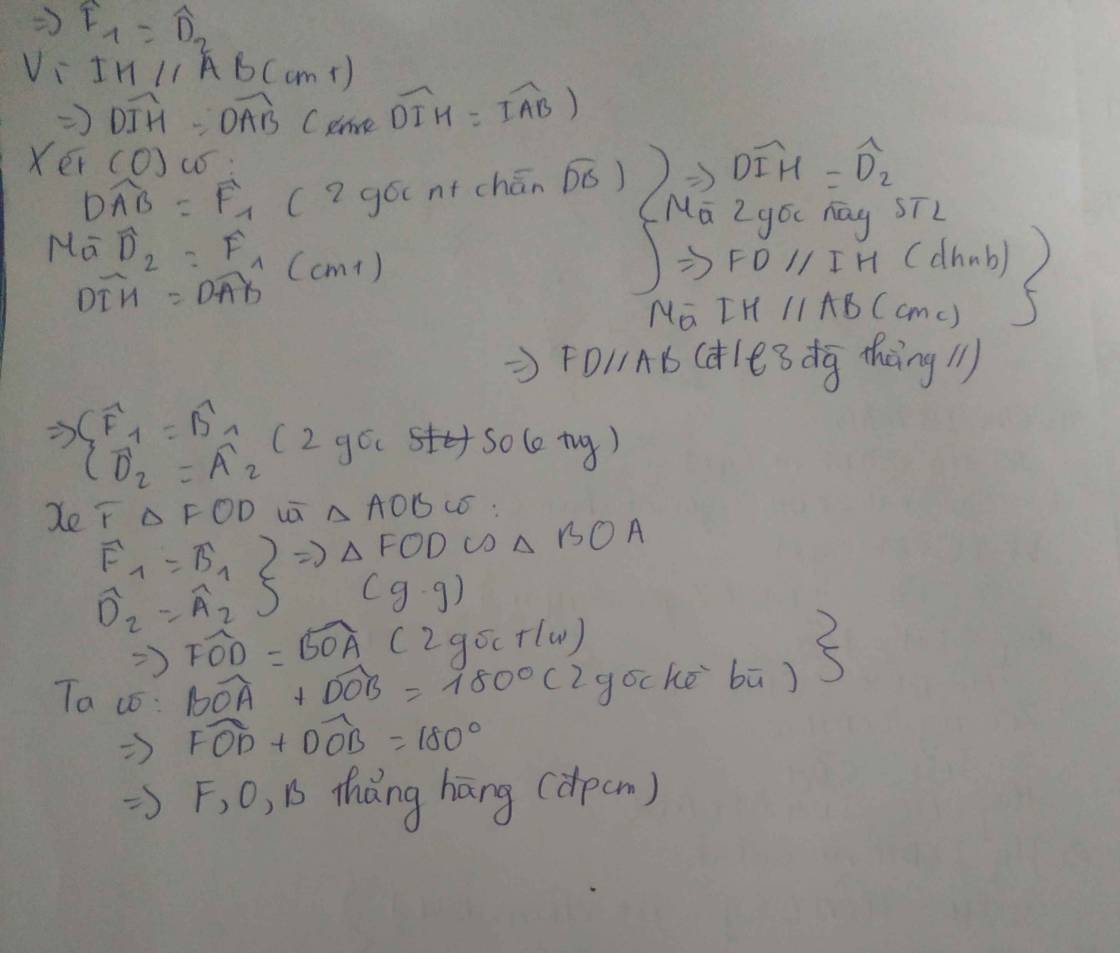
a) Kẻ DP là tiếp tuyến của (O) tại P. DP cắt d1 tại C'.
Trong đường tròn (O) có 2 tiếp tuyến tại P và B cắt nhau tại D nên OD là phân giác của \(\widehat{BOP}\)
Tương tự, ta có OC' là phân giác của \(\widehat{AOP}\). Do 2 góc BOP và AOP kề bù nên \(OC'\perp OD\). Lại có \(OC\perp OD\) và \(C,C'\in d_1\) nên \(C\equiv C'\). Như vậy CD chính là tiếp tuyến của đường tròn (O).
b) Theo tính chất 2 tiếp tuyến cắt nhau: \(AC=CP;BD=DP\). Do đó \(AC+BD=CP+DP\ge2\sqrt{CP.DP}\)
Mặt khác tam giác OCD vuông tại O có đường cao OP nên \(OP^2=CP.DP\Leftrightarrow\sqrt{CP.DP}=OP\)
Gọi R là bán kính của (O), khi đó
\(AC+BD\ge2OP=2R\). Dấu "=" xảy ra khi \(CP=DP\) \(\Leftrightarrow\sqrt{CP.CP}=OP\Leftrightarrow CP=OP\Leftrightarrow AC=R\)
Vậy để \(AC+BD\) nhỏ nhất thì C nằm trên d1 thỏa mãn \(AC=R\)
c) Ta có \(AC.BD=CP.DP=OP^2=a^2\)