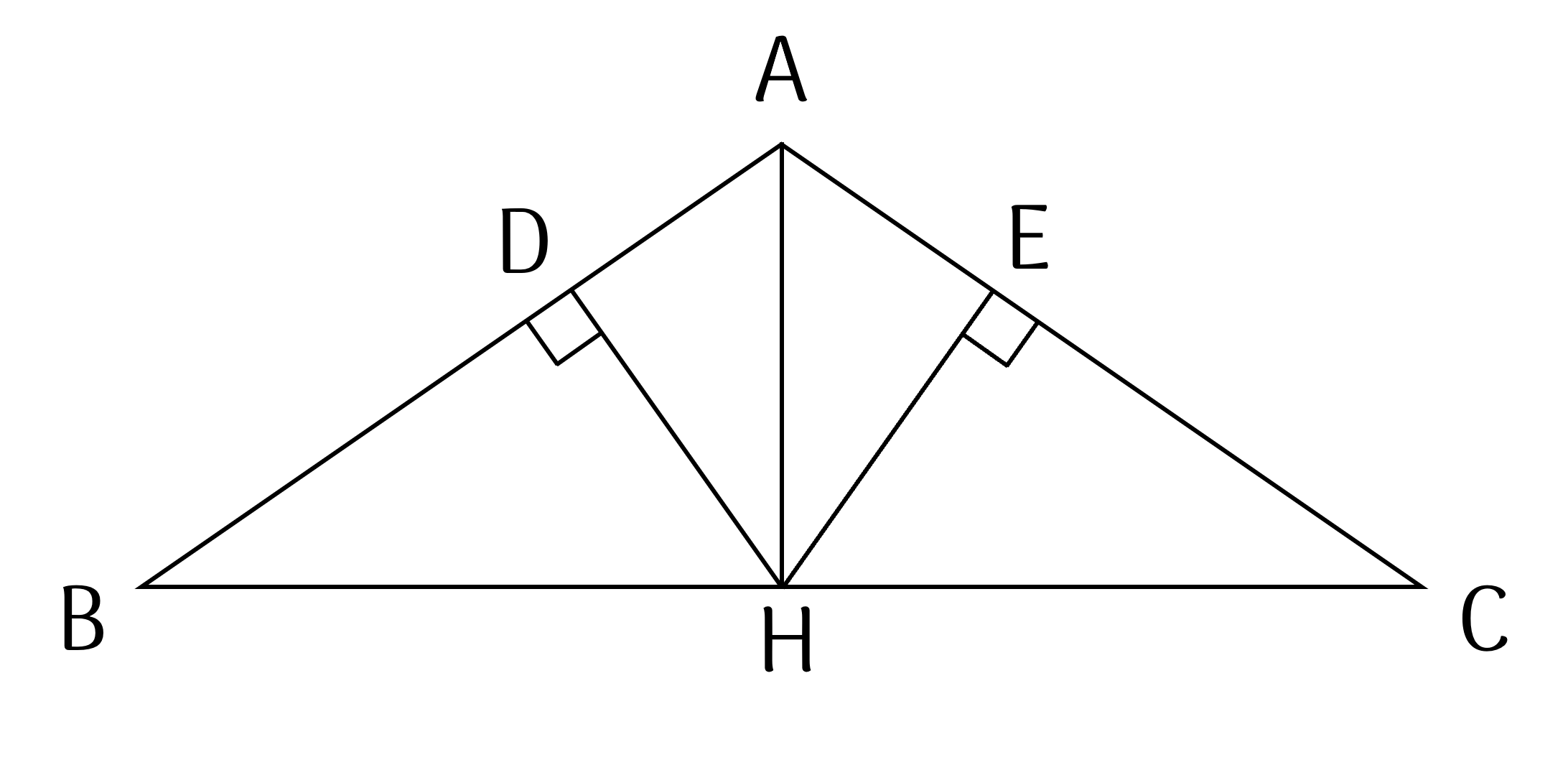
Cho tam giác ABC cân tại A kẻ AH vuông góc với BC (h thuộc BC).
a)Chứng minh góc Bah = CAH
b) Tính AC biết AH = 3cm, BC = 8cm.
c) Kẻ HE vuông góc với AB, HD vuông góc với AC. Chứng minh rằng HE = HD.
d)Chứng minh rằng ED song song với BC.
e) ọi giao điểm của AH và ED là M. Chứng minh rằng MH là phân giác của góc BAC và góc BMC.


Trả lời
a) Ta có:
AB = AE + EB
AC = AD + DC
Mà AB = AC (gt)
=> EB = DC
Xét ΔBDCΔBDC và ΔCEBΔCEB có:
EB = DC (cmt)
góc BDC = góc CEB = 900
BC là cạnh chung
Vậy: ΔBDCΔBDC = ΔCEBΔCEB (cạnh huyền - cạnh góc vuông)
b) Ta có: BC = BH + HC
=> BH = HC = BC2BC2 = 8282= 4 (cm)
Áp dụng định lí Py - ta - go vào ΔAHCΔAHC vuông tại H có:
AC2 = AH2 + HC2
AC2 = 32 + 42
AC2 = 9 + 16
AC2 = 25
AC = 25−−√25= 5 (cm)