Cho tam giác ABC nhọn, các đường cao BD và CE. Chứng minh góc ABC = góc ADE cắt đường cao BD và CE Bạn nào giải nhanh giúp mk với nha, mk đang gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Xét Δ ABD và Δ ABE, có :
\(\widehat{ADB}=\widehat{AEB}=90^o\)
\(\widehat{BAD}=\widehat{BAE}\) (góc chung)
=> Δ ABD ∾ Δ ABE (g.g)
b, Xét Δ EHB và Δ DHC, có :
\(\widehat{EHB}=\widehat{DHC}\) (đối đỉnh)
\(\widehat{HEB}=\widehat{HDC}=90^o\)
=> Δ EHB ∾ Δ DHC (g.g)
=> \(\dfrac{EH}{DH}=\dfrac{HB}{HC}\)
=> \(HB.HD=HC.HE\)

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
\(\widehat{BAD}\) chung
Do đó:ΔABD\(\sim\)ΔACE
Suy ra: AB/AC=AD/AE
hay \(AB\cdot AE=AD\cdot AC\)
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
\(\widehat{DAE}\) chung
Do đó:ΔADE\(\sim\)ΔABC
Suy ra: \(\widehat{ADE}=\widehat{ABC}\)

a) + ΔABD ∼ ΔACE ( g.g )
⇒ABAD=ACAE⇒ABAC=ADAE⇒ABAD=ACAE⇒ABAC=ADAE
b) + ΔBHE ∼ ΔCHD ( g.g )
⇒HBHE=HCHD⇒HBHE=HCHD
⇒HB⋅HD=HC⋅HE⇒HB⋅HD=HC⋅HE
c) + ΔADE ∼ ΔABC ( c.g.c )
⇒ADEˆ=ABCˆ

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc EDC+góc EBC=180 độ

Xét BEDC nội tiếp của đường tròn.
\(\widehat{EDB}=\widehat{ECB}\left(\text{cung BQ}\right)\)
Xét (O) có: \(\widehat{BPQ}=\widehat{EDB}\)
=> 2 góc này ở vị trí đồng
=> OA // DE
P/s: Ko chắc đâu
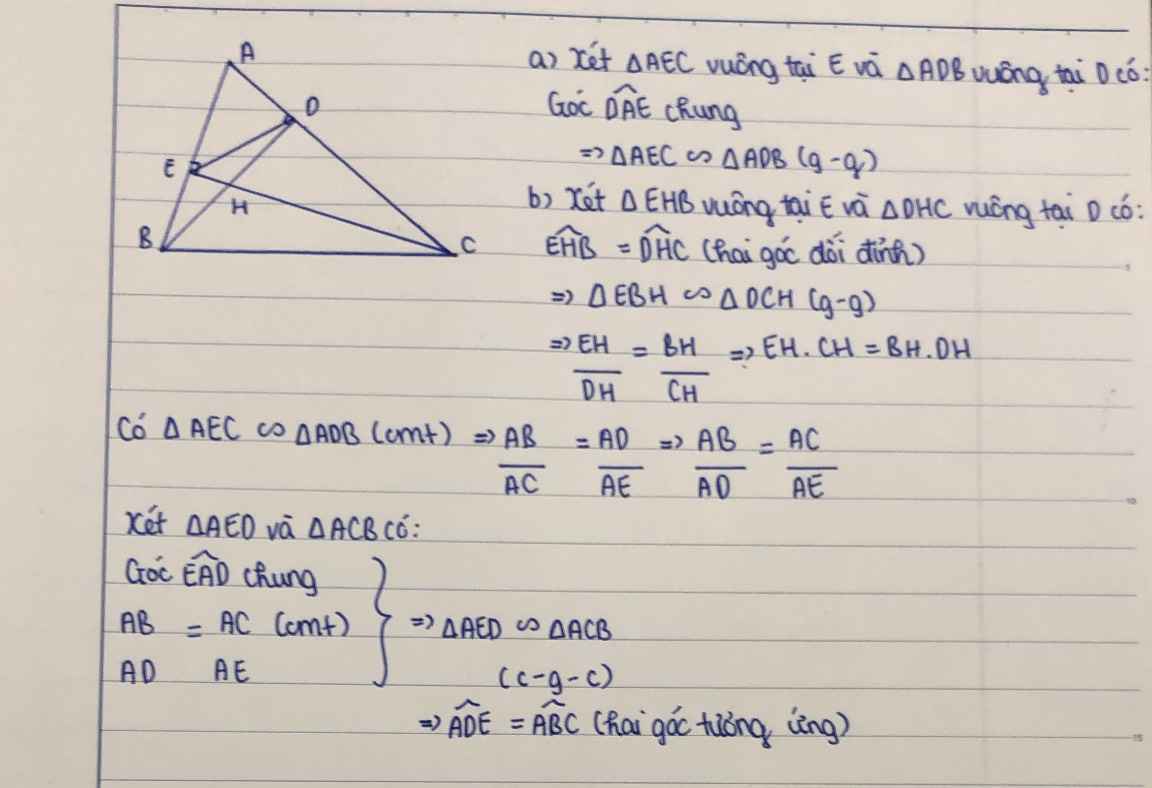

Không lẠm