cho hinh vẽ biết ^a+ ^B +^y=180độ. cmr: Ax // By
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 7 2017
1)
Vẽ tia Bz sao cho Bz//Ax (1)
Từ (1)\(\Rightarrow\widehat{xAE}=\widehat{AEz}\) (2)
Ta có: Ax//By (3)
Từ (1) và (3) \(\Rightarrow\) Ez//By (4)
Từ (4) \(\Rightarrow\widehat{yBE}=\widehat{BEz}\) (5)
Từ (2) và (5) \(\Rightarrow\widehat{xAE}=\widehat{AEz}=\widehat{yBE}=\widehat{BEz}\)
\(\Rightarrow\widehat{ABE}=\widehat{EAx}+\widehat{EBy}\) hay \(\widehat{AEB}=\widehat{A}+\widehat{B}\) (ĐPCM)
2) Tương tự.
14 tháng 8 2017
Vẽ tia Ez//Ax (như hình)
a) Ta có: Ax//By (đề cho)
Ax//Ez (theo cách vẽ Ez)
=> Ez//By
Ta có: Ax//By => góc A=góc E1 (so le trg)
Ez//By => góc B= góc E2 (so le trg)
Mà: E1+E2=góc AEB (1)
E1+E2=A+B (như chứng minh trên) (2)
Từ (1) và (2) suy ra góc AEB=góc A+góc B
b) Vẽ tia Ez//Ax (như hình)
Ta có: AEB=E1+E2
AEB=A+B
A+B=E1+E2
Ta có:Ez//Ax => A=E1 (so le trg)
=> B=E2
Ta có: E2=B là 2 góc so le trg nên Ez//By (1)
Mà Ez//Ax (2)
Từ (1) và (2) suy ra Ax//By (đpcm)
NU
0
5 tháng 12 2021
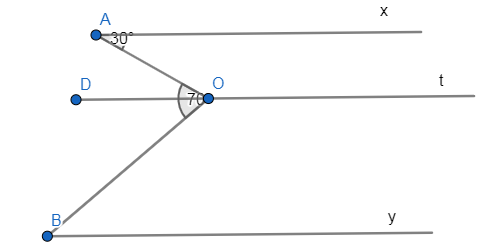
a, Kẻ Ot sao cho Ot song song với Ax và By, ta có:
\(\widehat{xAO}=\widehat{AOD}\) (So le trong)
\(\Rightarrow\widehat{xAO}=\widehat{AOD}=30^0\\\Rightarrow\widehat{DOB}=70^0-30^0=40^0\)
Mà OD//By
\(\Rightarrow\widehat{B}=\widehat{DOB}=40^0\)
3 tháng 10 2021
a: \(ax+by+cz\)
\(=x^3-xyz+y^3-xyz+z^3-xyz\)
\(=x^3+y^3+z^3-3xyz\)
3 tháng 10 2021
b: \(ax+by+cz\)
\(=x^3+y^3+z^3-3xyz\)
\(=\left(x+y\right)^3+z^3-3xy\left(x+y\right)-3yxz\)
\(=\left(x+y+z\right)\left(x^2+y^2+2xy-xz-yz+z^2\right)-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)
AH
Akai Haruma
Giáo viên
21 tháng 8 2023
Lời giải:
Ta thấy:
$\widehat{yBA}+\widehat{BAx}=124^0+56^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Ax$ (đpcm)
NT
1
MT
22 tháng 6 2015
(a2+b2) (x2+y2)=(ax+by)2
<=>a2x2+a2y2+b2x2+b2y2=a2x2+2axby+b2y2
<=>a2x2+a2y2+b2x2+b2y2-a2x2-2axby-b2y2=0
<=>a2y2+b2x2-2aybx=0
<=>(ay-bx)2=0
<=>ay-bx=0
<=>ay=bx
=>a/x=b/y