tìm nghiệm 4x-12:2x+32=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
Đặt t = 2x > 0 phương trình đã cho thành : t2 + (x - 7) t - 4x + 10 = 0 (1)
Coi (1) là phương trình bậc hai ẩn t, ta có
∆ = (x - 7) 2 - 4( -4x + 12) = (x + 1) 2 ≥ 0
Do đó (1) 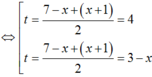
+ TH1. T = 4 thì 2x = 4 nên x = 2
+ TH2. T = 3 thì t = 3 - x và 2x = 3 - x, theo câu trên ta được x = 1
Tóm lại, phương trình đã cho có nghiệm là 1 và 2.

Lời giải:
Ta thấy:
$3x^2-4x+12=x^2+(2x^2-4x+2)+10=x^2+2(x^2-2x+1)+10$
$=x^2+2(x-1)^2+10\geq 10>0$ với mọi $x$
Do đó đa thức $3x^2-4x+12$ vô nghiệm.

Đặt t = x 2 - 2 x = 3 = x - 1 2 + 2 ≥ 2 ta được phương trình
t 2 + 2 3 - m t + m 2 - 6 m = 0 1
∆ ' = m 2 - 6 m + 9 - m 2 + 6 m = 9 suy ra phương trình (1) luôn có hai nghiệm là
t 1 = m - 6 v à t 2 = m
Theo yêu cầu bài toán ta suy ra phương trình (1) có nghiệm lớn hơn hoặc bằng 2
⇔ m − 6 ≥ 2 m ≥ 2 ⇔ m ≥ 2
Đáp án cần chọn là: D

Đặt t = x 2 - 2 x + 3 = x - 1 2 + 2 ≥ 2 ta được phương trình
t 2 + 2 3 - m t + m 2 - 6 m = 0 1
∆ ' = m 2 - 6 m + 9 - m 2 + 6 m = 9 suy ra phương trình (1) luôn có hai nghiệm là
t = m - 6 v à t 2 = m
Theo yêu cầu bài toán ta suy ra phương trình (1) phải có cả hai nghiệm nhỏ hơn 2
⇔ m < 8 m < 2 ⇔ m < 2
Đáp án cần chọn là: A
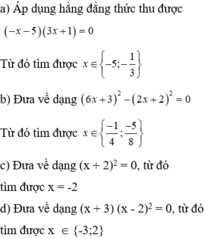
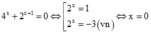
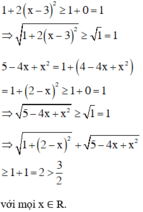
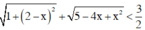 vô nghiệm.
vô nghiệm.
\(t^3+32t-12=0\)xem lại đề thôi