1. Cho hai góc AOB và A'OB' có các tia phân giác tương ứng là OC và OC'. Chứng minh rằng nếu OA và OA' là hai tia đối nhau, OC và OC' là hai tia đối nhau thì OB và OB' cũng là hai tia đối nhau.
2. Trên dường thẳng AA' lấy một điểm O. Trên nửa mặt phẳng có bờ là đường thẳng AA', ta kẻ các tia OB và OX. gọi Om là tia phân giác của góc AOB. Biết XOA= ao , XOB=bo (a>b). Hãy tính các góc AOB và XOM ( xét hai trường hợp tia OB nằm giữa hai tia OA, OX và OX nằm giữa hai tia OA và OB)
cần gấp!! giúp iem với a:<<
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

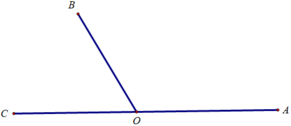
Ta có hai góc B O C ^ và A O B ^ kề bù nên B O C ^ + A O B ^ = 180o
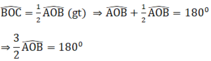
⇒ A O B ^ = 120o

a) Do BOC và AOB là 2 góc kề bù
=> OA ; OC là 2 tia đối nhau
Do AOD và AOB là 2 góc kề bù
=> OD ; OB là 2 tia đối nhau
=> BOC và AOD là 2 góc đối đỉnh (dpcm)
b) ?????????????

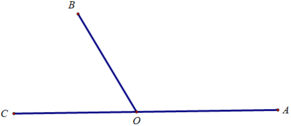
Ta có hai góc ∠BOC và ∠AOB kề bù nên ∠BOC + ∠AOB = 180o
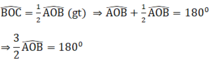

(hình tự vẽ)
a, Ta có: \(\widehat{AOB}+\widehat{BOC}=180^o\)
\(\Rightarrow3\widehat{BOC}+\widehat{BOC}=180^o\)
\(\Rightarrow4\widehat{BOC}=180^o\)
\(\Rightarrow\widehat{BOC}=45^o\)
\(\Rightarrow\widehat{AOC}=3\widehat{BOC}=3.45^o=135^o\)
b, Ta có: \(\widehat{AOD}+\widehat{DOB}=135^o\)
\(\Rightarrow90^o+\widehat{DOB}=135^o\)
\(\Rightarrow\widehat{DOB}=45^o\)
Mà \(\widehat{BOC}=45^o\)
\(\Rightarrow\widehat{DOB}=\widehat{BOC}=45^o\)
Và OB nằm giữa OD, OC
=> OB là tia p/g của \(\widehat{COD}\)

a/ chia góc aoc làm 8 phần
theo đề: aob bằng 7 lần boc => aob chiếm 7/8 và boc chiếm 1/8
(giải theo cách tổng tỉ)
vậy aob = 160 . 7/8 = 140
và boc = 160. 1/8 = 20
b/ vì aoc > cod =>od nằm giữa oa,oc
nên:aod = 160 - 90 = 70
vì aod < aob => od nằm giữa oa,ob
nên: bod = 140 - 70 = 70
vì aod + bob = aob và aod = bod = 70