Tìm n thỏa mãn 1n+2n+......+50n > 51n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 4 2018
Ta có 2 2 n + 1 = 1 + 1 2 n + 1 = C 2 n + 1 0 + C 2 n + 1 1 + ... + C 2 n + 1 2 n + 1 . (1)
Lại có C 2 n + 1 0 = C 2 n + 1 2 n + 1 ; C 2 n + 1 1 = C 2 n + 1 2 n ; C 2 n + 1 2 = C 2 n + 1 2 n − 1 ; . . . ; C 2 n + 1 n = C 2 n + 1 n + 1 . (2)
Từ (1) và (2), suy ra C 2 n + 1 0 + C 2 n + 1 1 + ... + C 2 n + 1 n = 2 2 n + 1 2
⇔ C 2 n + 1 1 + ... + C 2 n + 1 n = 2 2 n + 1 2 − C 2 n + 1 0
⇔ C 2 n + 1 1 + ... + C 2 n + 1 n = 2 2 n − 1 ⇔ 2 20 − 1 = 2 2 n − 1 ⇔ n = 10 .
Vậy n =10 thỏa mãn yêu cầu bài toán.
Chọn đáp án C.
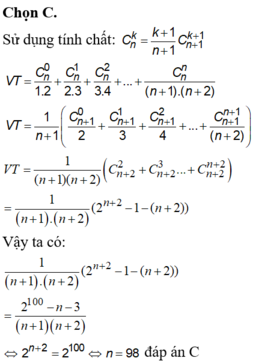
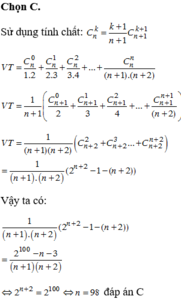
ta có 1^n =1^n ; 2^n>1^n ; 3^n>1^n;.......;50^n>1^n
nên 1^n+2^n+3^n+4^n+5^n+....50^n> 51*1^n=51^n