cho tam giác ABC có AB=3cm AC=4cm.Độ dài đường cao AH là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có tam giác vuông ABC=> AB2+AC2=BC2(do BC là cạnh huyền)
Mà AB=3cm; AC=4cm ta đc
32+42=BC2
=>9+16=BC2
=>BC=5(cm)
Diện tích hình tam giác là: 3.4/2=6(cm2)
Độ dài AH là: 6.2/5=2,4cm
Vậy AH=2,4cm


Theo mình:
Tam giác ABC vuông tại A
---> BA là đường cao ( BA vuông góc AC)
---> S tam giác ABC = \(\frac{a.h}{2}=\frac{AC.BC}{2}=\frac{4.3}{2}=6cm^2\)
Pytago tam giác ABC vuông tại A:
BC2 = BA2 + AC2
= 9 + 16
= 25
BC= 5 cm
Vì AH cũng là đường cao của tam giác ABC
----> AH = \(\frac{2.S}{a}=\frac{2.6}{BC}=\frac{12}{5}=2,4cm\)
Theo mình thì mình làm vậy á, nếu mình làm sai thì bạn sửa giùm mình nha

A B H C
xét tam giác ABC vuông ở A co \(BC^2=AB^2+AC^2\left(pitago\right)\)
\(BC^2=9+16=25\Rightarrow BC=5\)
xet tgABH va tgCBA co goc B chung ; gAHB=gBAC =90
=>tgABH đồng dạng tgCBA =>\(\frac{AH}{AC}=\frac{AB}{BC}\Leftrightarrow\frac{AH}{4}=\frac{3}{5}\Rightarrow AH=\frac{3\cdot4}{5}=\frac{12}{5}\)


a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
a. Xét ΔHBA và ΔABC có:
\(\widehat{H}=\widehat{A}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) ΔHBA \(\sim\) ΔABC (g.g)
b. Vì ΔABC vuông tại A
Theo đ/lí Py - ta - go ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42
\(\Rightarrow\) BC2 = 25 cm
\(\Rightarrow\) BC = \(\sqrt{25}=5\) cm
Ta lại có: ΔHBA \(\sim\) ΔABC
\(\dfrac{AH}{CA}=\dfrac{BA}{BC}\)
\(\Leftrightarrow\dfrac{AH}{4}=\dfrac{3}{5}\)
\(\Rightarrow\) AH = 2,4 cm

\(S_{AHC}=\dfrac{AH\cdot HC}{2}=\dfrac{2.4\cdot3.2}{2}=2.4\cdot1.6=3.84\left(cm^2\right)\)
Xét \(\Delta ABC\) vuông tại A có
\(BC^2=AB^2+AC^2=25\)
\(\Rightarrow BC=5\left(cm\right)\)
AC\(^2\) = CH . CB = 5 CH
\(\Rightarrow CH=3,2\left(cm\right)\)
AB . AC = AH . BC \(\Rightarrow AH=2,4\)
Nên \(S_{AHC}=\dfrac{1}{2}.AH.CH=\dfrac{1}{2}.2,4.3,2=3,84\left(cm^2\right)\)

a:\(BC=\sqrt{4^2+3^2}=5\left(cm\right)\)
AH=4*3/5=2,4cm
b: ΔCAD cân tại C
mà CH là đường cao
nên CH là phân giác của góc ACD
Xét ΔCAB và ΔCDB có
CA=CD
góc ACB=góc DCB
CB chung
Do dó: ΔCAB=ΔCDB
=>góc CDB=90 độ
=>BD là tiếp tuyến của (C)

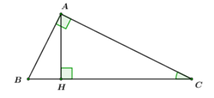
Áp dụng định lý Pytago trong ∆ ABC vuông tại A ta có:
![]()
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
![]()
![]()
Đáp án cần chọn là: B
5 cm nha bạn
Chúc các bạn học giỏi
Tết vui vẻ nha
Độ dài AH là 2,4 nhé bạn...chứ không phải 5