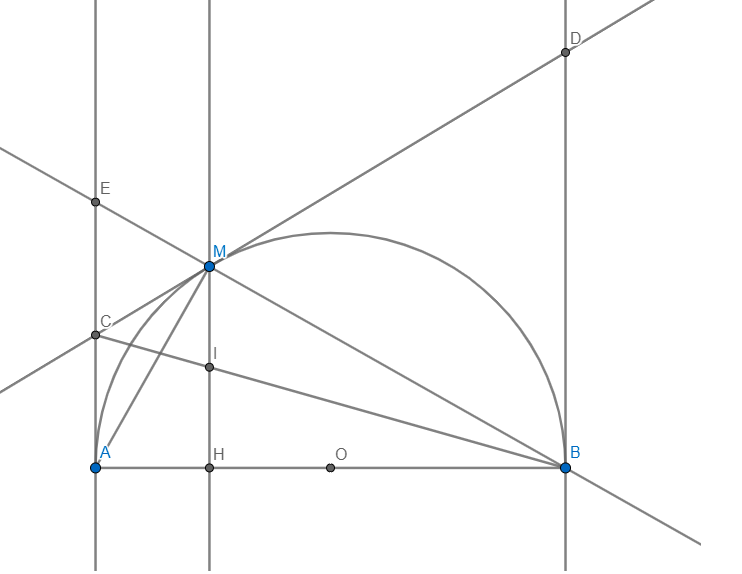
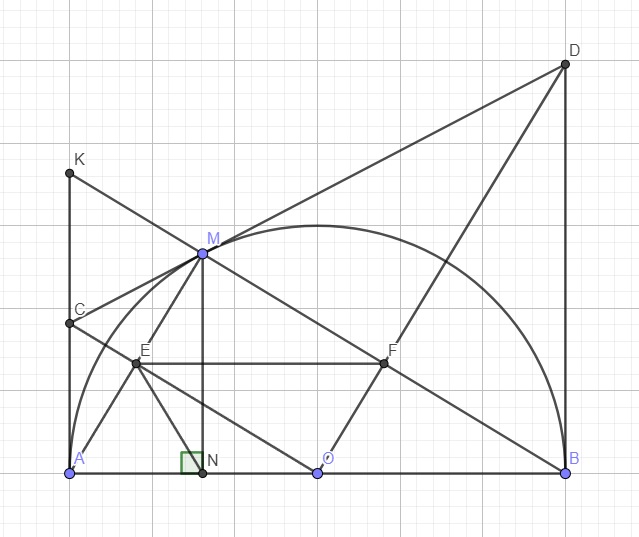
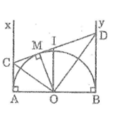
CHo nửa đường tròn tâm O đường Kính AB. Vẽ 2 tiếp tuyến Ax và By cùng nửa mặt phẳng vs đường tròn. Lấy M trên nửa đường tròn. Tiếp tuyến tại M cắt Ax và By tại C, D.
- tìm vị trí của M để AC+BD nhỏ nhất
- AM song song với OD
- gọi I, N là giao điểm của AM với CO, BM với OD. CMR tứ giác MION là hình chữ nhật
- AB tiếp xúc với đường tròn đường kính CD
- IN là đường trung bình tam giác MAB
- gọi I' là giao điểm của OM với Ax. CMR: I'C.OD = I'O.CO
- Tam giác AMB là tam giác vuông
- tam giác IAO đồng dạng với tam giác NOB
- Gọi R là bán kính của (O), r là bán kính đường tròn nội tiếp tam giác COD.CMR: 2<R/r<3
- Gọi K là giao điểm của AD với BC. MK cắt AB tại H. CMR: MH vuông góc với AB
- Tìm vị trí của M để tam giác MHO lớn nhất
- kéo dài CO cắt DB tại Q. CMR: tam giác DCQ cân tại D
- Gọi D', E', F' là giao điểm của CD với AB, BM với Ax, D'E' với By. CMR: A, M, F' thẳng hàng
- 2MH2 = MA.MB
- CB,AD,IN,MH đồng quy
- gọi L là giao điểm của EA và DO. CMR: DEL là tam giác cân