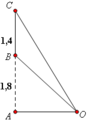
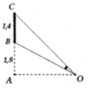
Xác định vị trí đặt mắt để nhìn thấy ảnh AB nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
25 tháng 4 2023
Ta có: \(\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}=\dfrac{OA}{12}\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{OI}{A'B'}=\dfrac{OF}{OF-OA'}=\dfrac{60}{60-12}=\dfrac{5}{4}\)
\(\Rightarrow\dfrac{OA}{12}=\dfrac{5}{4}\Rightarrow OA=\dfrac{12.5}{4}=15\left(cm\right)\)
Vậy khi đeo kính nhiìn vật AB vị trí đặt vật gần mắt nhất để nhìn rõ là 15cm
CM
31 tháng 10 2019
Đáp án A
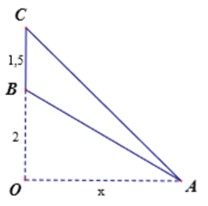
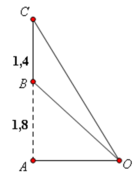
Phương pháp giải: Dựa vào hệ thức lượng trong tam giác và công thức lượng giác xác định độ lớn của góc cần tính thông qua khoảng cách. Khảo sát hàm số tìm min – max
Lời giải: Với bài toán này, ta cần xác định OA để góc BOC lớn nhất. Điều này xảy ra khi tan BOC lớn nhất.
Đặt OA = x(m) với x > 0. Ta có:
30 tháng 10 2015
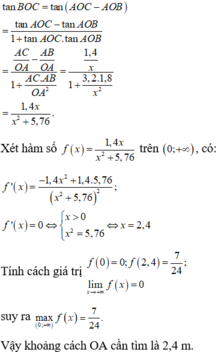
a) Mắt muốn nhìn thấy ảnh S' của S qua gương thì phải có tia sáng từ ảnh S' qua gương đến mắt.
Ta có hình vẽ
Ảnh S' đối xứng với S qua gương
Tam giác S'NM đồng dạng với ONI
\(\Rightarrow\frac{NM}{NI}=\frac{S'M}{IO}=\frac{120}{40}=3\)
Mà NM + NI = MI = 50 cm
\(\Rightarrow IN=\frac{50}{4}=12,5>10\)cm
Nên đường đi của tia sáng ra ngoài bề rộng của gương, do vậy người này không nhìn thấy ảnh của S.
b) Để nhìn thấy ảnh của S thì N phải tiến lại gần mép gương, do đó người phải tiến lại gần gương sao cho N có vị trí mới thỏa mãn: NI = 10cm.
Khi đó NM = 40 cm.
Lại xét hai tam giác đồng dạng ở trên, ta có: \(\frac{S'M}{IO}=\frac{NM}{NI}=\frac{40}{10}=4\)
Suy ra: IO = 120/4 = 30cm.
Vị trí mới của O cách gương 30 cm, nên khoảng cách từ vị trí ban đầu đến vị trí mắt bắt đầu nhìn thấy ảnh S' là: 40-30 =10cm.
VT
25 tháng 1 2017
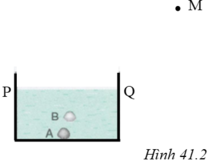
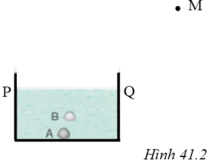
Trên hình 41.2 SGK cho biết M là vị trí đặt mắt để nhìn thấy ảnh viên sỏi nhỏ ở trong nước, A là vị trí thực của viên sỏi, B là vị trí ảnh của nó, PQ là mặt nước. Hãy vẽ đường truyền của tia sáng từ viên sỏi đến mắt.
VT
28 tháng 2 2018
Đáp án: C
HD Giải:
Khi ngắm chừng ở cực cận:
+ d2’ = - OCC = - 20 cm
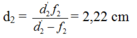
+ d1’ = O1O2 – d2 = 12,78 cm
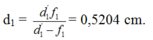
Khi ngắm chừng ở cực viễn:
+ d2’ = - OCV = -50
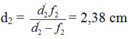
+ d1’ = O1O2 – d2 = 12,62 cm;
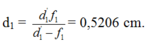
Phải đặt vật cách vật kính trong khoảng:
