cho tam giác ABC có: AB = AC , M là trung điểm của BC , trên tia đối của tia MA lấy điểm D sao cho AM = MD. chứng minh:
a) tam giác ABM= tam giác DCM
b) AB // DC
c) AM vuông góc với BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 4 2021
a) Xét ΔABM và ΔDCM có
MB=MC(M là trung điểm của BC)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MA=MD(gt)
Do đó: ΔABM=ΔDCM(c-g-c)
5 tháng 4 2021
b) Ta có: ΔABM=ΔDCM(cmt)
nên AB=CD(Hai cạnh tương ứng)
mà AB<AC(gt)
nên CD<AC
Xét ΔACD có
CD<AC(cmt)
mà góc đối diện với cạnh CD là \(\widehat{CAD}\)
và góc đối diện với cạnh AC là \(\widehat{ADC}\)
nên \(\widehat{CAD}< \widehat{ADC}\)(Định lí quan hệ giữa góc và cạnh đối diện trong tam giác)
\(\Leftrightarrow\widehat{CAM}< \widehat{MDC}\)
mà \(\widehat{BAM}=\widehat{MDC}\)(ΔABM=ΔDCM)
nên \(\widehat{BAM}>\widehat{CAM}\)(đpcm)
17 tháng 1 2022
a: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó:ABDC là hình bình hành
Suy ra: AB//DC
c: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
15 tháng 12 2023
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
b: Xét ΔMBA vuông tại M và ΔMCD vuông tại M có
MB=MC
MA=MD
Do đó: ΔMBA=ΔMCD
=>\(\widehat{MBA}=\widehat{MCD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
c: Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
\(\widehat{MBE}=\widehat{MCF}\)
Do đó: ΔBEM=ΔCFM
=>ME=MF
ΔBEM=ΔCFM
=>\(\widehat{BME}=\widehat{CMF}\)
mà \(\widehat{BME}+\widehat{EMC}=180^0\)(hai góc kề bù)
nên \(\widehat{CMF}+\widehat{EMC}=180^0\)
=>F,M,E thẳng hàng
mà MF=ME
nên M là trung điểm của EF
21 tháng 12 2023
a: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM
b: ta có: ΔABM=ΔDCM
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DC
c: Xét ΔMEB vuông tại E và ΔMFC vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)(hai góc đối đỉnh)
Do đó: ΔMEB=ΔMFC
=>ME=MF
mà M nằm giữa E và F
nên M là trung điểm của EF
4 tháng 4 2023
`a)`
Có `AM` là trung tuyến `=>M` là tđ `BC=>BM=CM`
Xét `Delta ABM` và `Delta DCM` có :
`{:(BM=CM(cmt)),(hat(M_1)=hat(M_2)(đối.đỉnh)),(AM=DM(Gt)):}}`
`=>Delta ABM=Delta DCM(c.g.c)(đpcm)`
`b)`
Có `Delta ABM=Delta DCM(cmt)`
`=>hat(A_1)=hat(D_1)(2` góc t/ứng `)`
mà `2` góc này ở vị trí Soletrong
nên `AB////CD(đpcm)`
`c)`
Có `AC>AB(GT)`
mà `AC` là cạnh đối diện của `hat(B_1)`
`AB` là cạnh đối diện của `hat(C_1)`
nên `hat(B_1)>hat(C_1)`(mối quan hệ góc và cạnh đối diện trong `Delta` )(đpcm)
4 tháng 1 2022
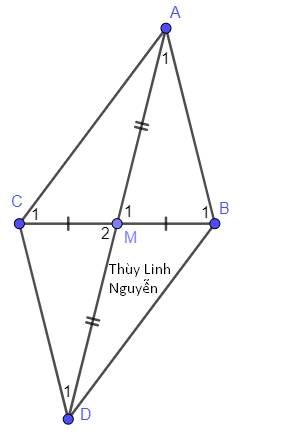
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Xét tứ giác ABKC có
M là trung điểm của BC
M là trung điểm của AK
Do đó: ABKC là hình bình hành
Suy ra: AB//KC
c: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
18 tháng 1 2022
a: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//DC
c: Ta có: ΔACB cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
a) xét tg ABM & tg DCM có
MB=MC (vì M là trung điểm BC)
AMB^ =DMC^(2 GÓC ĐỐI ĐỈNH)
MA =MD (GT)
=) tg ABM=tg DCM(c.g.c)
vậy.......
b) Vì tg ABC =TG DCM nên ABM^ =DCM^ (2 góc tương ứng)
Mà ABM^ & DCM^ ở vị trí so le trong nên AB//DC
vậy.....
c)Xét tg ABM& ACM có
AB =AC (gt)
AM là cạnh chung
BM =CM( vì M là trung điểm BC)
=) tg ACM =ABM(C.c.c)
=) AMB^ =AMC^ ( 2 góc tương ứng)
Mà AMB^ +AMC=180 (2 góc kề bù )
nên AMB^ =AMC=90
=) AM vuông góc vs BC
mk đã làm chi tiết lắm đó Vân Khánh
good luck