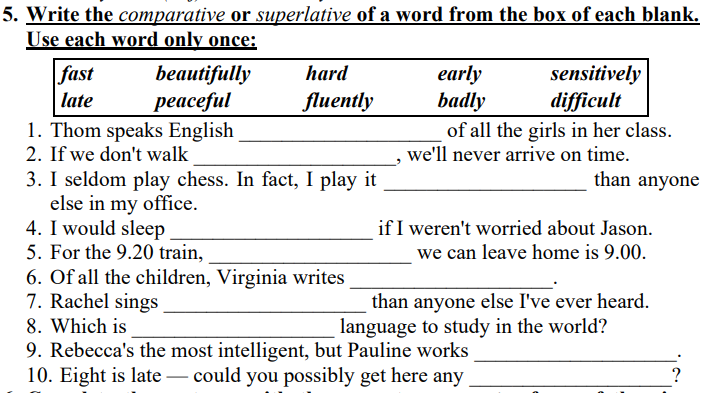
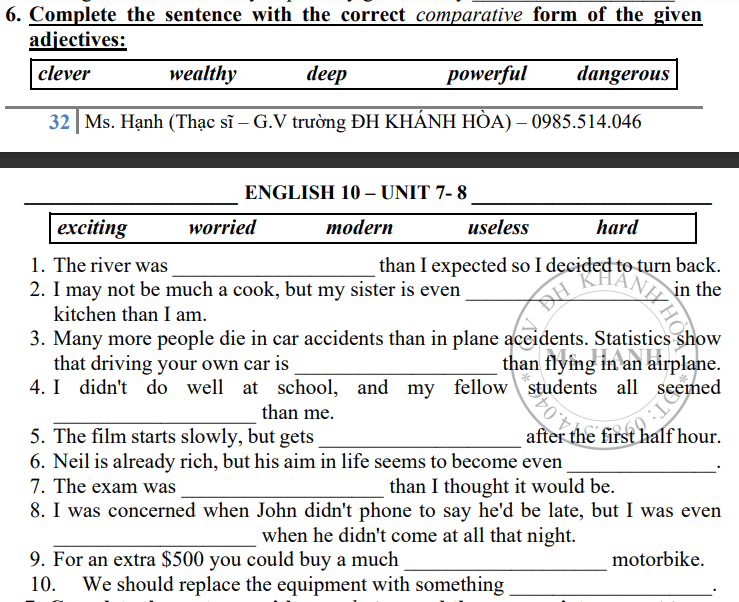
giúp e câu38 này với ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bạn đăng tách ra tầm 10 câu mỗi lần đăng nha, chứ dài ntnay ngại làm lắm~
e có tách 3 bài ra rồi ạ, phiền anh/chị/bạn giúp e với ạ, e cảm ơn ạ


chu vi hình vuông là
50x4=200cm
độ dài 1 cạnh hình vuông là
50:4=12,5cm
diện tích hình vuông là
12,5x12,5=156,25cm2

a: \(P=\dfrac{8}{x\left(x+4\right)}+\dfrac{5x}{x\left(x+4\right)}-\dfrac{2x+8}{x\left(x+4\right)}=\dfrac{8+5x-2x-8}{x\left(x+4\right)}=\dfrac{3}{x+4}\)
b: Thay x=1/2 vào P, ta được:
P=3:9/2=3x2/9=6/9=2/3
Với khác 0 ; x khác 4
\(P=\dfrac{8+5x-2x-8}{x\left(x+4\right)}=\dfrac{3x}{x\left(x+4\right)}=\dfrac{3}{x+4}\)
Thay x = 1/2 vào P ta được \(\dfrac{3}{\dfrac{1}{2}+4}=\dfrac{3}{\dfrac{9}{2}}=3:\dfrac{9}{2}=\dfrac{2}{3}\)

a, \(n_{CaCO_3}=\dfrac{41,2}{100}=0,412\left(mol\right)\)
PTHH: CaO + H2O → Ca(OH)2
Mol: 0,412 0,412
PTHH: Ca(OH)2 + CO2 → CaCO3 + H2O
Mol: 0,412 0,412 0,412
\(m_{CaO}=0,412.56=23,072\left(g\right)\)
b, \(V_{CO_2}=0,412.22,4=9,2288\left(l\right)\)
\(m_{Na_2CO_3}=100.16,96\%=16,96\left(g\right)\Rightarrow n_{Na_2CO_3}=\dfrac{16,96}{106}=0,16\left(mol\right)\)
\(m_{BaCl_2}=200.10,4\%=20,8\left(g\right)\Rightarrow n_{BaCl_2}=\dfrac{20,8}{208}=0,1\left(mol\right)\)
PTHH: Na2CO3 + BaCl2 → BaCO3 + 2NaCl
Mol: 0,1 0,1 0,2
Ta có: \(\dfrac{0,16}{1}>\dfrac{0,1}{1}\) ⇒ Na2CO3 dư, BaCl2 hết
mdd sau pứ = 100 + 200 = 300 (g)
\(C\%_{ddNaCl}=\dfrac{0,1.58,5.100\%}{300}=1,95\%\)
\(C\%_{ddNa_2CO_3}=\dfrac{\left(0,16-0,1\right).106.100\%}{300}=2,12\%\)


a, văng vẳng, quang quác quác, tè te te
Tác dụng: Cho thấy sự huyên náo của các loài vật trong rừng núi, nó làm bức tranh thiên nhiên trở nên sinh động và đẹp hơn
b, đùng đùng, vù vù, lộp độp
Tác dụng: Cho thấy những dấu hiệu trước cơn mưa, cơn mưa diễn ra nhanh chóng và mạnh






 giúp e 2 câu này với ạ e sắp phải nộp rùi ạ
giúp e 2 câu này với ạ e sắp phải nộp rùi ạ
Xét \(I_1=\int\limits^{\dfrac{\pi}{3}}_{\dfrac{\pi}{4}}\dfrac{f\left(tanx\right)}{cos^2x}dx=\int\limits^{\dfrac{\pi}{3}}_{\dfrac{\pi}{4}}f\left(tanx\right)d\left(tanx\right)\)
Đặt \(tanx=t\Rightarrow t\in\left[1;\sqrt{3}\right]\Rightarrow f\left(t\right)=2t^3-t\)
\(I_1=\int\limits^{\sqrt{3}}_1f\left(t\right)dt=\int\limits^{\sqrt{3}}_1\left(2t^3-t\right)dt=3\)
Xét \(I_2=\int\limits^{\sqrt{e-1}}_0\dfrac{xf\left(ln\left(x^2+1\right)\right)}{x^2+1}dx=\dfrac{1}{2}\int\limits^{\sqrt{e-1}}_0f\left(ln\left(x^2+1\right)\right).d\left[ln\left(x^2+1\right)\right]\)
Đặt \(ln\left(x^2+1\right)=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=-3t+4\)
\(I_2=\dfrac{1}{2}\int\limits^1_0\left(-3t+4\right)dt=\dfrac{5}{4}\)
\(\Rightarrow I=3+\dfrac{5}{4}=\dfrac{17}{4}\Rightarrow P=21\)