Cho tam giác ABC cân tại A. Có AB=10 cm, BC=12 cm. Kẻ BH vuông góc AC (H thuộc AC). Tính BH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

27 tháng 6 2023
a: ΔABC cân tại A có AH là phân giác
nên H là trung điểm của BC
ΔABC cân tại A có AH là trung tuyến
nên AH vuông góc BC
b: BH=CH=12/2=6cm
AH=căn AB^2-AH^2=8cm
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
=>ΔADH=ΔAEH
=>AD=AE và HD=HE
=>ΔHDE cân tại H
d: Xét ΔABC có AD/AB=AE/AC
nên DE//BC

30 tháng 4 2023
a: Xet ΔAHB vuông tại H và ΔAKC vuông tại K có
góc BAH chung
AB=AC
=>ΔAHB=ΔAKC
=>AH=AK
=>ΔAHK cân tại A
b: góc ABH+góc HBC=góc ABC
gócACK+góc ICB=góc ACB
mà góc ABC=góc ACB; góc ABH=góc ACK
nên góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác của góc BIC
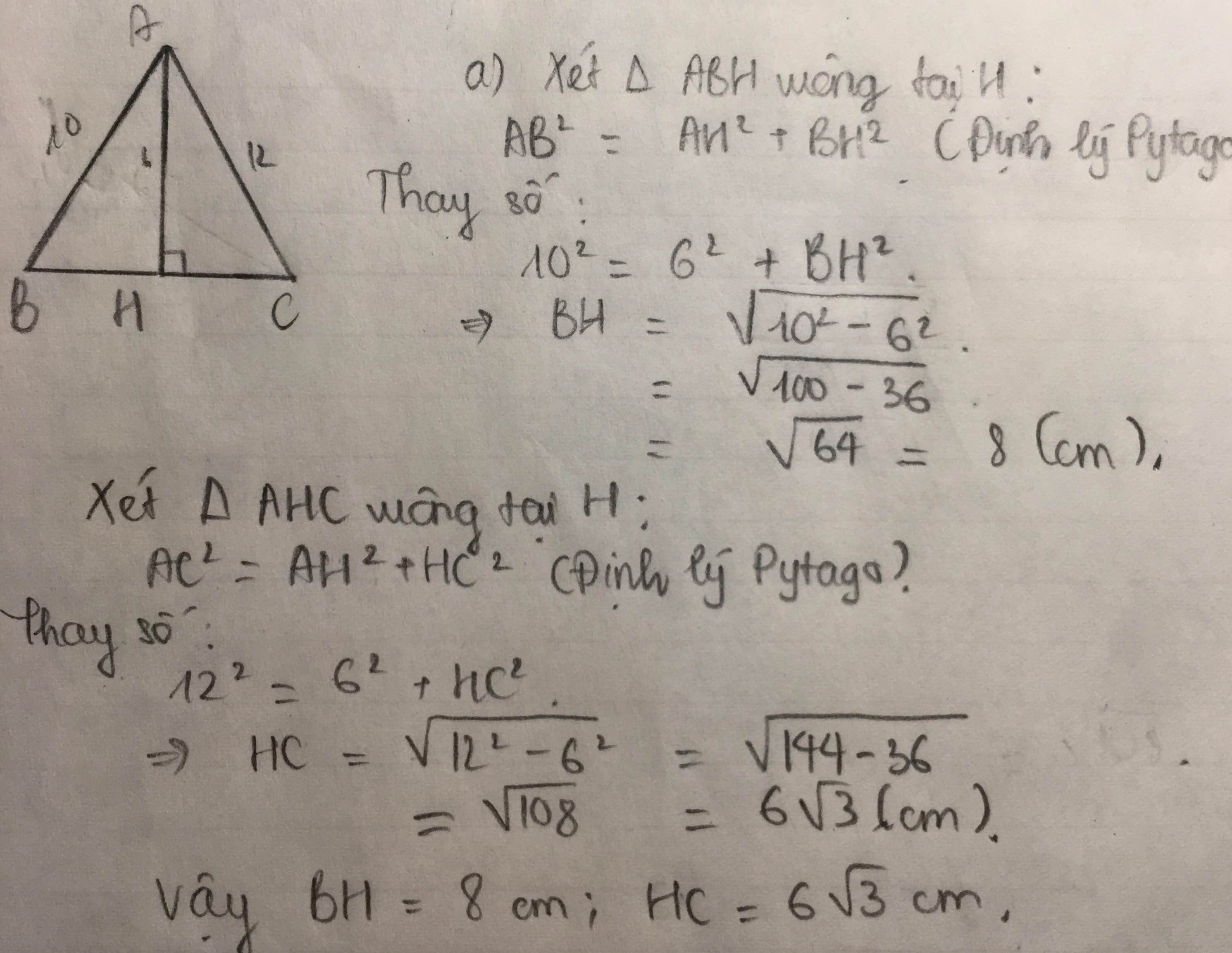
hi
Kẻ đường cao AK ứng với cạnh BC ( K thuộc BC )
+) Xét \(\Delta ABC\) cân tại A có : AK là đường cao ứng với BC
=> AK đồng thời là đường trung trực của BC
\(\Rightarrow BK=KC=\dfrac{1}{2}BC=\dfrac{1}{2}.12=6\left(cm\right)\)
+) Áp dụng định lí Py - ta - go vào \(\Delta AKB\left(\widehat{AKB}=90^o\right)\) , có :
\(AK^2=AB^2-BK^2\)
\(\Leftrightarrow AK=\sqrt{10^2-6^2}=8\left(cm\right)\)
+) Ta có : \(S_{\Delta ABC}=S_{\Delta ABH}+S_{\Delta BHC}\)
\(\Leftrightarrow\dfrac{1}{2}AH.BC=\dfrac{1}{2}BH.AH+\dfrac{1}{2}BH.HC\)
\(\Leftrightarrow8.12=BH\left(AH+HC\right)\)
\(\Leftrightarrow BH.AC=96\left(cm\right)\)
\(\Leftrightarrow BH=\dfrac{96}{10}=9,6\left(cm\right)\)