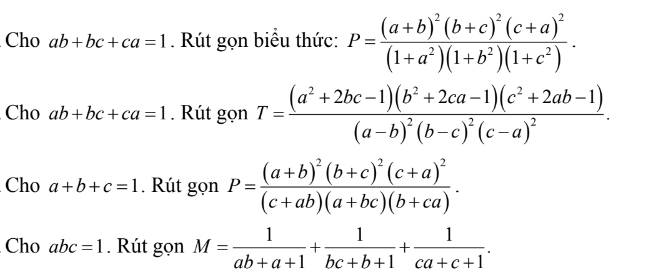Giups mình với ạ Minh đg cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
0
DN
1
5 tháng 10 2021
\(W=\dfrac{1}{2}\left(\sqrt{\left(2+\sqrt{2}\right)^2}+\sqrt{\left(2-\sqrt{2}\right)^2}\right)\\ W=\dfrac{1}{2}\left(2+\sqrt{2}+2-\sqrt{2}\right)=\dfrac{1}{2}\cdot4=2\\ Y=\dfrac{1}{2}\left(\sqrt{\left(4+\sqrt{3}\right)^2}+\sqrt{\left(4-\sqrt{3}\right)^2}\right)\\ Y=\dfrac{1}{2}\left(4+\sqrt{3}+4-\sqrt{3}\right)=\dfrac{1}{2}\cdot8=4\)
HT
4
DN
1
5 tháng 10 2021
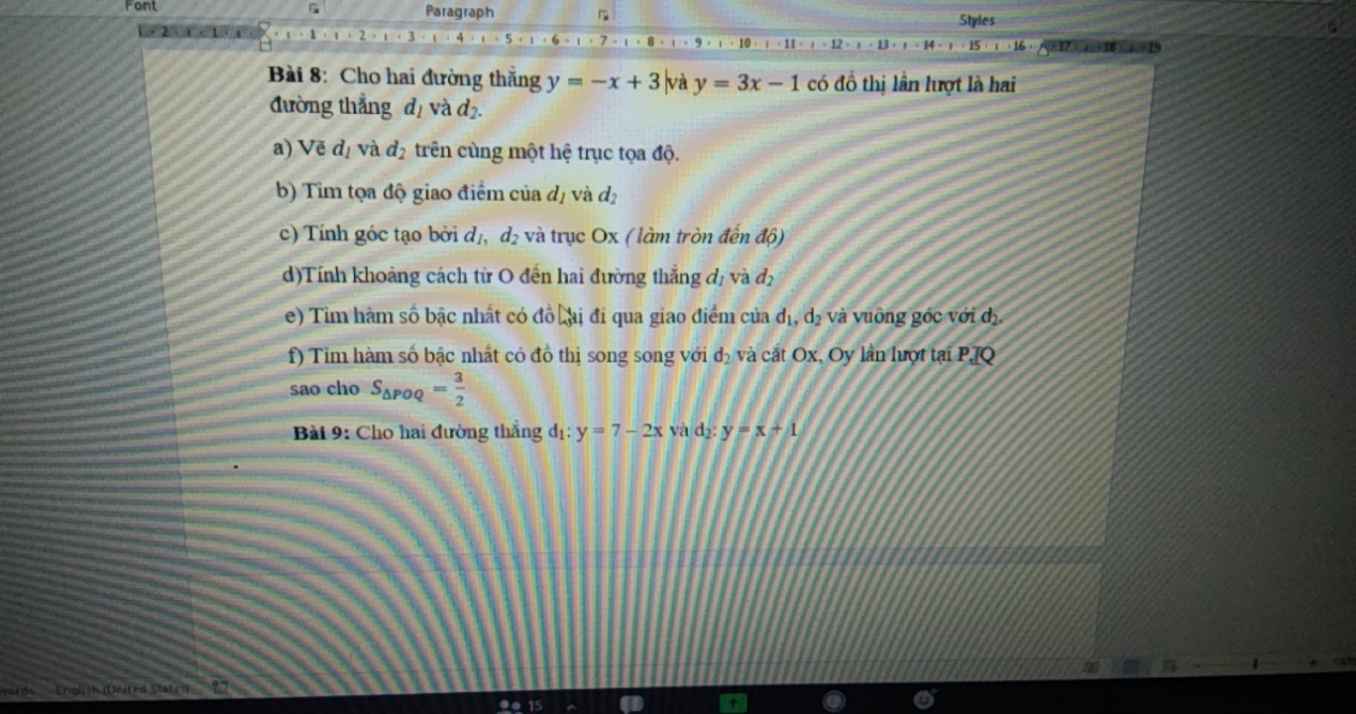
Bài 8:
b: Phương trình hoành độ giao điểm là:
\(-x+3=3x-1\)
\(\Leftrightarrow-4x=-4\)
hay x=1
Thay x=1 vào (d), ta được:
y=-1+3=2
AC
5
NA
30 tháng 9 2018
\(\frac{4x}{1-x^2}=\sqrt{5}\) ĐKXĐ : x khác 1
\(\Rightarrow4x=\sqrt{5}\left(1-x^2\right)\)
\(\Leftrightarrow4x=\sqrt{5}-x^2\sqrt{5}\)
\(\Leftrightarrow x^2\sqrt{5}-4x-\sqrt{5}=0\)
\(\Leftrightarrow x^2\sqrt{5}-5x+x-\sqrt{5}=0\)
\(\Leftrightarrow x\sqrt{5}\left(x-\sqrt{5}\right)+\left(x-\sqrt{5}\right)=0\)
\(\Leftrightarrow\left(x-\sqrt{5}\right)\left(x\sqrt{5}+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-\sqrt{5}=0\\x\sqrt{5}=-1\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\sqrt{5}\left(tmđk\right)\\x=-\frac{1}{\sqrt{5}}=-\frac{\sqrt{5}}{5}\left(tmđk\right)\end{cases}}}\)
30 tháng 9 2018
\(4x=\sqrt{5}-\sqrt{5}x^2\)
\(\Rightarrow4x+\sqrt{5}x^2=\sqrt{5}\)
\(\Rightarrow x\left(4+\sqrt{5}x\right)=\sqrt{5}\)
\(\Rightarrow x.\sqrt{5}\left(\frac{4}{\sqrt{5}}+x\right)=\sqrt{5}\)
\(\Rightarrow x.\left(\frac{4}{\sqrt{5}}+x\right)=1\)
Với x = 1 \(\Rightarrow\frac{4}{\sqrt{5}}+x=1\Rightarrow x=1-\frac{4}{\sqrt{5}}=\frac{5-4\sqrt{5}}{5}\)
Với x = -1\(\Rightarrow\frac{4}{\sqrt{5}}+x=-1\Rightarrow x=-1-\frac{4}{\sqrt{5}}=-\frac{5+4\sqrt{5}}{5}\)
ko có x thỏa mãn
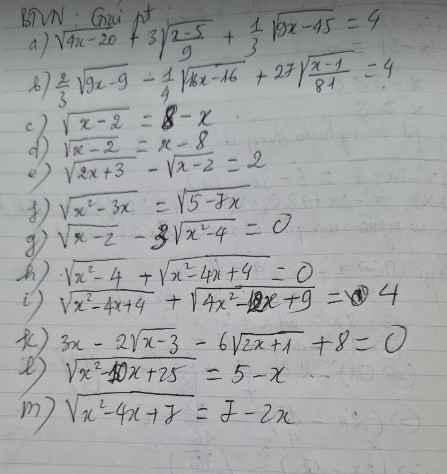
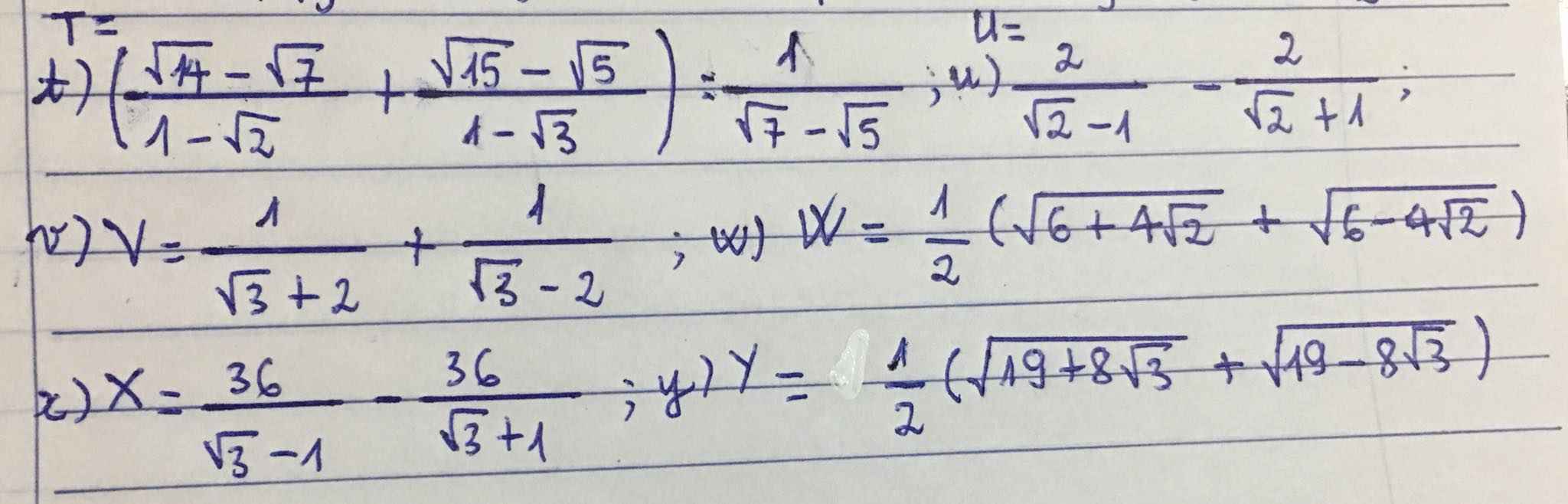
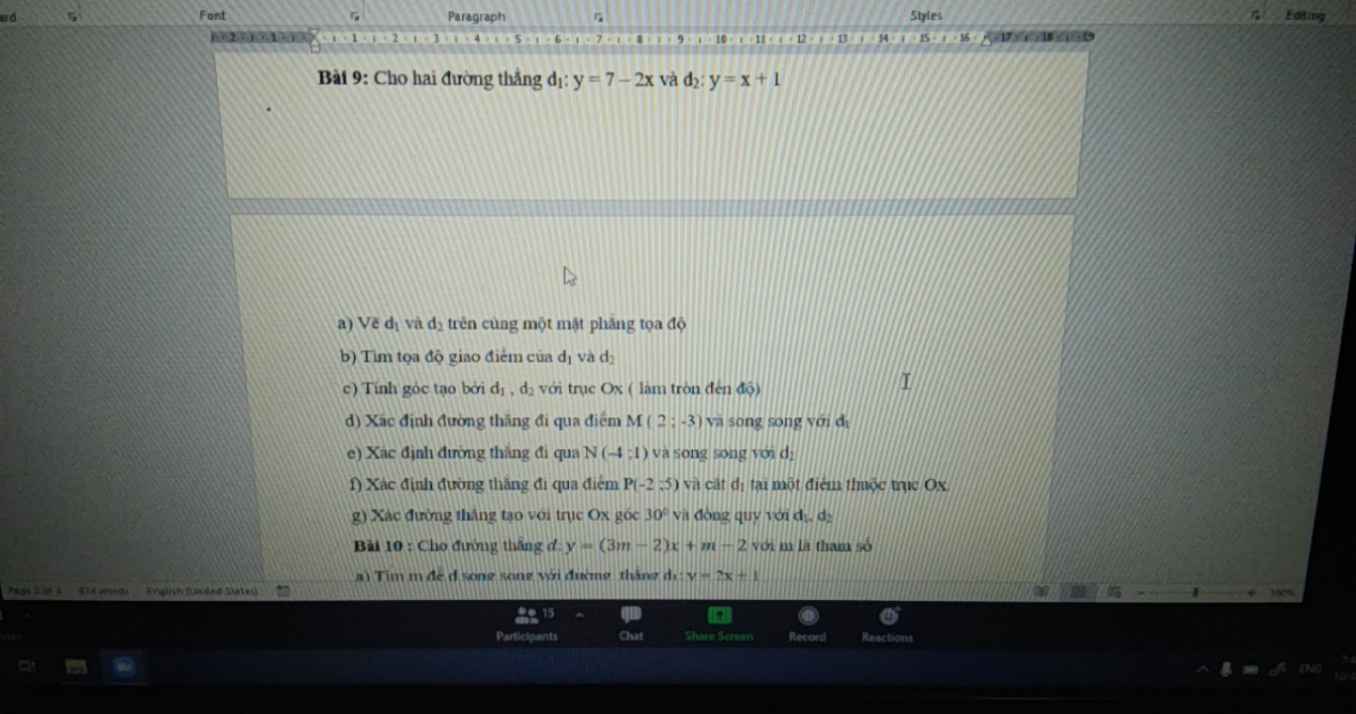
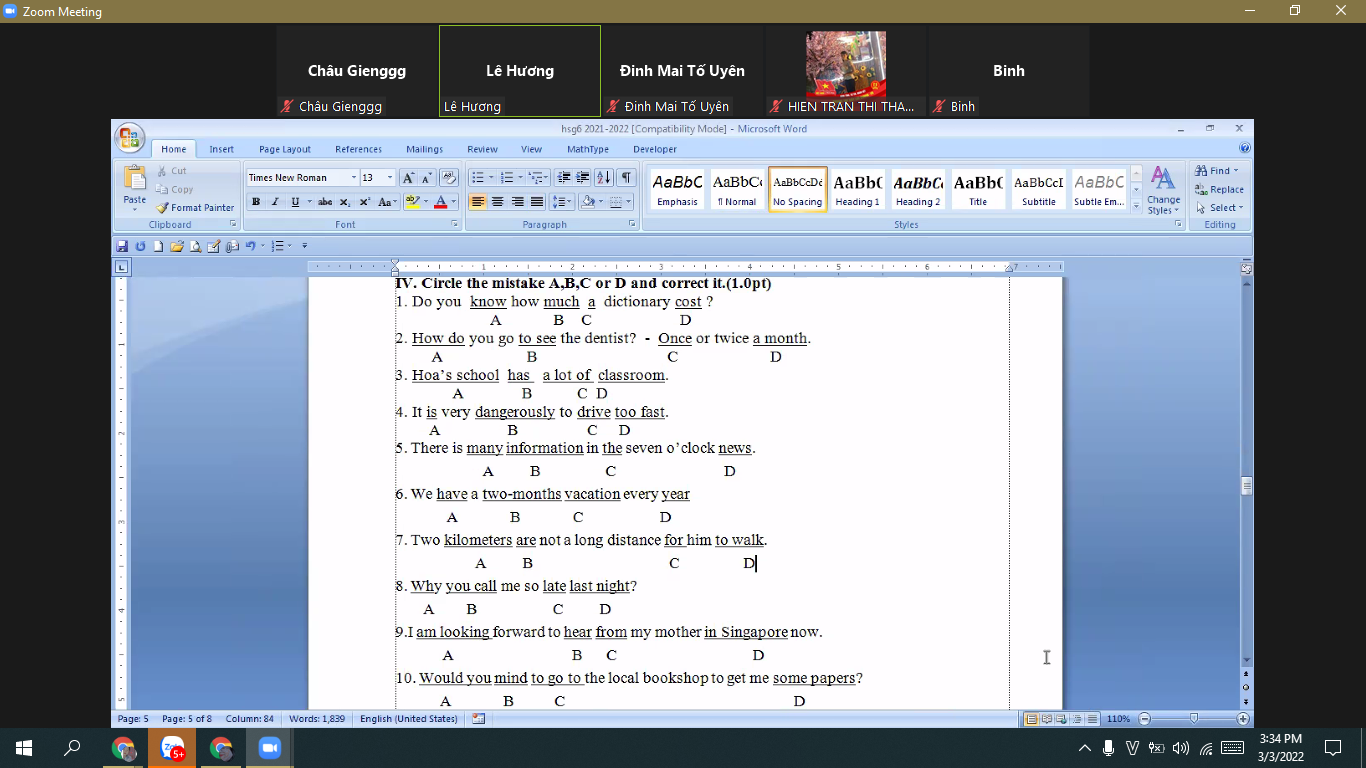
2 câu đầu của bạn như bạn này mik giải rồi nhá
https://olm.vn/hoi-dap/detail/6617747567939.html
+) \(P=\dfrac{\left(a+b\right)^2\left(b+c\right)^2\left(c+a\right)^2}{\left(c+ab\right)\left(a+bc\right)\left(b+ca\right)}\)
\(=\dfrac{\left(a+b\right)^2\left(b+c\right)^2\left(c+a\right)^2}{\left(c\left(a+b+c\right)+ab\right)\left(a\left(a+b+c\right)+bc\right)\left(b\left(a+b+c\right)+ca\right)}\)
\(=\dfrac{\left(a+b\right)^2\left(b+c\right)^2\left(c+a\right)^2}{\left(c^2+ab+bc+ca\right)\left(a^2+ab+bc+ca\right)\left(c^2+ab+bc+ca\right)}\)
\(=\dfrac{\left(a+b\right)^2\left(b+c\right)^2\left(c+a\right)^2}{\left(a+b\right)^2\left(b+c\right)^2\left(c+a\right)^2}=1\)
+) \(M=\dfrac{1}{ab+a+1}+\dfrac{1}{bc+b+1}+\dfrac{1}{ca+c+1}\)
\(=\dfrac{1}{ab+a+1}+\dfrac{abc}{bc+ab^2c+abc}+\dfrac{abc}{ca+c+abc}\left(vìabc=1\right)\)
\(=\dfrac{1}{ab+a+1}+\dfrac{abc}{bc\left(ab+a+1\right)}+\dfrac{abc}{c\left(ab+a+1\right)}\)
\(=\dfrac{ab+a+1}{ab+a+1}=1\)