abc + a + b + c =243
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta chứng minh 2 bất đẳng thức phụ sau: với x, y, z dương thì:
\(x^4+y^4+z^4\ge xyz\left(x+y+z\right)\left(1\right)\)
\(\left(1+x\right)\left(1+y\right)\left(1+z\right)\ge\left(1+\sqrt[3]{xyz}\right)^3\left(2\right)\)
+ Chứng minh BĐT (1), sử dụng BĐT AM - GM:
\(x^4+x^4+y^4+z^4\ge4x^2yz\)
\(y^4+y^4+x^4+z^4\ge4xy^2z\)
\(z^4+z^4+x^4+y^4\ge4xyz^2\)
Cộng dồn lại ta có: \(x^4+y^4+z^4\ge xyz\left(x+y+z\right)\)
+ Chứng minh BĐT (2). Ta có:
\(\left(1+x\right)\left(1+y\right)\left(1+z\right)=1+x+y+z+xy+yz+xyz\ge1+3\sqrt[3]{xyz}+3\sqrt[3]{x^2y^2z^2}+xyz=\left(1+\sqrt[3]{xyz}\right)^3\)
Bây giờ ta quay lại chứng minh BĐT ở đề.
BĐT cần chứng minh tương đương với BĐT sau:
\(\sqrt[4]{\left(1+\dfrac{1}{a}\right)^4+\left(1+\dfrac{1}{b}\right)^4+\left(1+\dfrac{1}{c}\right)^4}\ge\sqrt[4]{3}+\dfrac{\sqrt[4]{243}}{2+abc}\)
\(\Leftrightarrow\left(1+\dfrac{1}{a}\right)^4+\left(1+\dfrac{1}{b}\right)^4+\left(1+\dfrac{1}{c}\right)^4\ge3\left(1+\dfrac{3}{2+abc}\right)^4\)
Sử dụng BĐT (1) ta có:
\(\left(1+\dfrac{1}{a}\right)^4+\left(1+\dfrac{1}{b}\right)^4+\left(1+\dfrac{1}{c}\right)^4\ge\left(1+\dfrac{1}{a}\right)\left(1+\dfrac{1}{b}\right)\left(1+\dfrac{1}{c}\right)\left(3+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\)
Sử dụng BĐT (2) và BĐT AM - GM ta có:
\(\left(1+\dfrac{1}{a}\right)\left(1+\dfrac{1}{b}\right)\left(1+\dfrac{1}{c}\right)\left(3+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge\left(1+\dfrac{1}{\sqrt[3]{abc}}\right)^3\left(3+\dfrac{3}{\sqrt[3]{abc}}\right)\)
\(\Rightarrow\left(1+\dfrac{1}{a}\right)\left(1+\dfrac{1}{b}\right)\left(1+\dfrac{1}{c}\right)\left(3+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge3\left(1+\dfrac{1}{\sqrt[3]{abc.1.1}}\right)^4\ge3\left(1+\dfrac{3}{2+abc}\right)^4\)
Vậy BĐT đã được chứng minh. Đẳng thức xảy ra <=> a = b = c.

a, 3 n . 3 = 243 => 3 n + 1 = 243 => 3 n + 1 = 3 5
=> n + 1 = 5 => n = 4
Vậy n = 4
b, 4 3 . 2 n + 1 = 1
=> 2 2 3 . 2 n + 1 = 1
=> 2 2 . 3 . 2 n + 1 = 1 => 2 6 . 2 n + 1 = 1
=> 2 6 + n + 1 = 1 => 2 n + 7 = 2 0
=> n + 7 = 0
Không tìm được số tự nhiên n thỏa mãn đầu bài
c, 2 n - 15 = 17
=> 2 n = 32 => 2 n = 2 5
=> n = 5
Vậy n = 5
d, 8 ≤ 2 n + 1 ≤ 64
=> 2 3 ≤ 2 n + 1 ≤ 2 6
=> 3 ≤ n + 1 và n+1 ≤ 6
=> 2 ≤ n và n ≤ 5
=> 2 ≤ n ≤ 5
Vậy 2 ≤ n ≤ 5
e, 9 < 3 n < 243
=> 3 2 < 3 n < 3 5
=> 2<n<5
Vậy 2<n<5

a)(167+35)+(134-167-35) b)(43-31+57)-(243-345+54) c)(89-76)+(76-89+28) d)(243+46-345)-(243-345+54)
=167+35+134-167-35 =43-31+51-43+345-54 =89-76+76-89+28 =243+46-345-243+345-54
=167-167+35-35+134 =12+51-43+345-54 =0+28 =289-345-243+345-54
=0+0+134 =63-43+291 =28 =(-56)-243+345-54
=134 =20+291=311 =(-299)+345-54
=46-54=-8

a, \(64:2^3\) = \(2^6:2^3\) = \(2^3=8\)
b, \(7^5:343=7^5:7^3=7^2=49\)
c, \(243:3^3:3=3^5:3^3:3=3^{ }\)
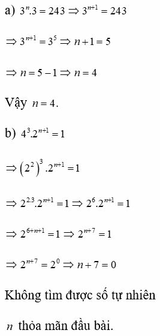
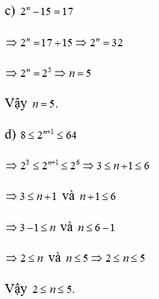
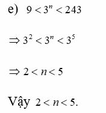
200+40+3+0=243