help mình với 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
7
HT
12
4 tháng 1 2023
a, (1) \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
(2) \(AlCl_3+3NaOH\rightarrow3NaCl+Al\left(OH\right)_{3\downarrow}\)
\(2Al\left(OH\right)_3\underrightarrow{t^o}Al_2O_3+3H_2O\)
(4) \(2Al_2O_3\underrightarrow{đpnc}4Al+3O_2\)
b, (1) \(2Fe+3Cl_2\underrightarrow{t^o}2FeCl_3\)
(2) \(FeCl_3+3NaOH\rightarrow3NaCl+Fe\left(OH\right)_{3\downarrow}\)
(3) \(2Fe\left(OH\right)_3\underrightarrow{t^o}Fe_2O_3+H_2O\)
(4) \(Fe_2O_3+3H_2\underrightarrow{t^o}2Fe+3H_2O\)
(5) \(Fe+2HCl\rightarrow FeCl_2+H_2\)
c, (1) \(2Al_2O_3\underrightarrow{đpnc}4Al+3O_2\)
(2) \(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\)
(3) \(Al_2\left(SO_4\right)_3+3BaCl_2\rightarrow3BaSO_{4\downarrow}+2AlCl_3\)
(4) \(AlCl_3+3NaOH\rightarrow3NaCl+Al\left(OH\right)_{3\downarrow}\)
d, (1) \(S+O_2\underrightarrow{t^o}SO_2\)
(2) \(2SO_2+O_2\xrightarrow[V_2O_5]{t^o}2SO_3\)
(3) \(SO_3+H_2O\rightarrow H_2SO_4\)
(4) \(H_2SO_4+2NaOH\rightarrow Na_2SO_4+2H_2O\)
(5) \(Na_2SO_4+BaCl_2\rightarrow2NaCl+BaSO_{4\downarrow}\)
e, (1) \(2Al_2O_3\underrightarrow{đpnc}4Al+3O_2\)
(2) \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
(3) \(AlCl_3+3NaOH\rightarrow3NaCl+Al\left(OH\right)_{3\downarrow}\)
(4)
(5) \(NaAlO_2+CO_2+2H_2O\rightarrow Al\left(OH\right)_{3\downarrow}+NaHCO_3\)
HT
5
IO
13 tháng 12 2021
3x . 2 + 15 = 33
3x . 2 = 33 - 15 = 18
3x = 18 : 2 = 9 = 32
=> x = 2
Y
11 tháng 7 2023
\(1,x=16\Rightarrow A=\dfrac{16-1}{\sqrt{16}}=\dfrac{15}{4}\)
\(2,B=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+4\sqrt{x}\left(dl:x>0,x\ne1\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2+4\sqrt{x}\left(x-1\right)}{x-1}\\ =\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1+4x\sqrt{x}-4\sqrt{x}}{x-1}\\ =\dfrac{4x\sqrt{x}}{x-1}\)
\(3,P=A.B=\dfrac{x-1}{\sqrt{x}}.\dfrac{4x\sqrt{x}}{x-1}=4x\)
\(\sqrt{P}>P\Leftrightarrow\sqrt{4x}>4x\Leftrightarrow\left(\sqrt{4x}\right)^2>\left(4x\right)^2\Leftrightarrow4x>16x^2\Leftrightarrow4x-16x^2>0\Leftrightarrow4x\left(1-4x\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x>0\\1-4x>0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x>0\\x< \dfrac{1}{4}\end{matrix}\right.\)
Vậy \(S=\left\{x|0< x< \dfrac{1}{4}\right\}\) thì \(\sqrt{P}>P\)
\(4,\left|P\right|>P\Leftrightarrow\left|4x\right|>4x\)
\(TH_1:x\ge0\\4x>4x\Leftrightarrow4x-4x>0\Leftrightarrow0>0\left(VL\right) \)
\(TH_2:x< 0\\ -4x>4x\Leftrightarrow-4x-4x>0\Leftrightarrow-8x>0\Leftrightarrow x< 0\)
Vậy \(x< 0\) thì \(\left|P\right|>P\)
XB
10 tháng 1 2023
Gọi \(x\) là số học sinh giỏi lớp 5A. Theo đề bài ta có:
\(x\) x \(\dfrac{3}{5}\) = 6 ⇒ \(x\) = 6 x \(\dfrac{5}{3}\) = 10 (học sinh)
Vậy lớp 5A có 10 học sinh giỏi
9 tháng 1 2023
Số học sinh lớp 5A là:
6 : \(\dfrac{3}{5}\)
= 10 ( em)
Đ/S: 10 em
19 tháng 12 2021
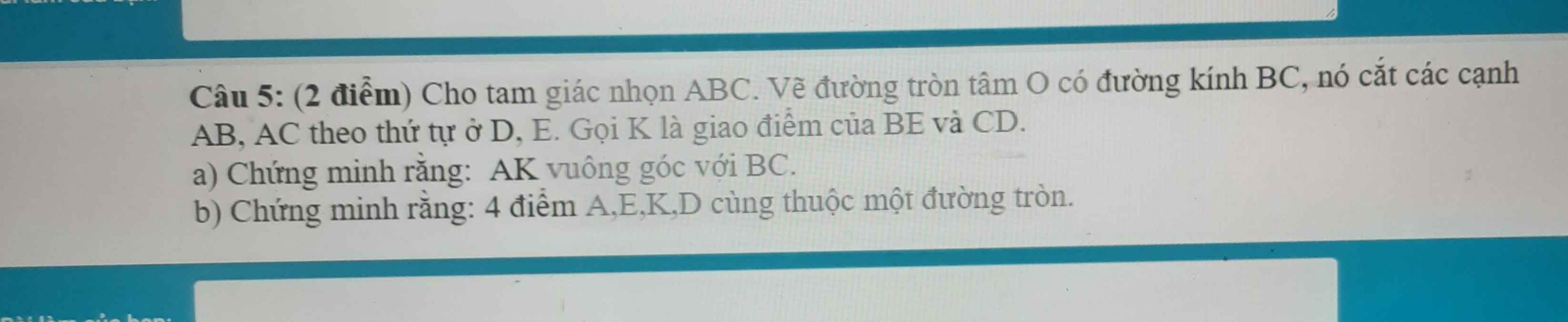
a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔEBC vuông tại E
Xét ΔABC có
BE là đường cao
CD là đường cao
BE cắt CD tại K
Do đó: AK⊥BC
27 tháng 12 2021
a: Xét ΔABE và ΔACE có
AB=AC
AE chung
BE=CE
Do đó: ΔABE=ΔACE
help mình với :(
5 tháng 1 2022
a: a⊥AB
b⊥AB
Do đó: a//b
b: \(\widehat{D_1}+\widehat{C_1}=180^0\)
nên \(\widehat{C_1}=60^0\)
3 tháng 3 2022
Bài 3:
a: Thay m=-1/2 vào (1),ta được:
\(x^2-2\cdot\left(2-\dfrac{1}{2}\right)x+2\cdot\dfrac{-1}{2}+1=0\)
\(\Leftrightarrow x^2-3x=0\)
=>x=0 hoặc x=3
b: \(\Delta=\left(2m+4\right)^2-4\left(2m+1\right)\)
\(=4m^2+16m+16-8m-4\)
\(=4m^2+8m+12\)
\(=4m^2+8m+4+8=\left(2m+2\right)^2+8>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow\left(2m+4\right)^2-2\left(2m+1\right)=6\)
\(\Leftrightarrow4m^2+16m+16-4m-2-6=0\)
\(\Leftrightarrow4m^2+12m+8=0\)
\(\Leftrightarrow\left(m+1\right)\left(m+2\right)=0\)
=>m=-1 hoặc m=-2
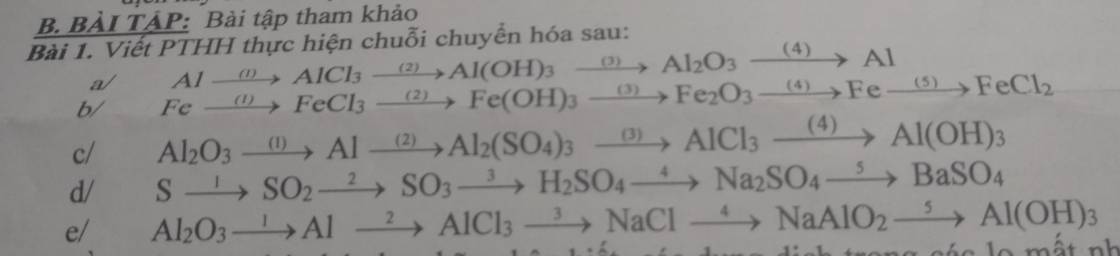
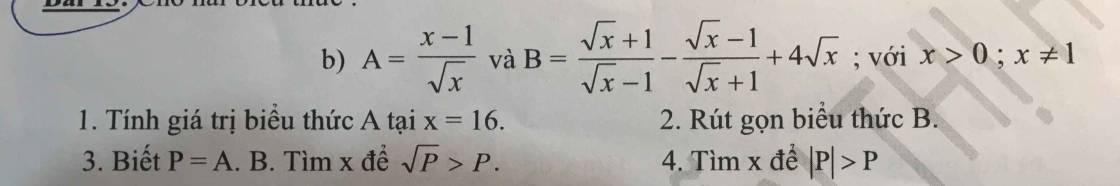
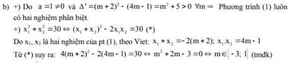
Quá trình trên là quá trình nóng chảy.
Vì nhiệt độ của vật ban đầu tăng lên, sau đó không đổi trong quá trình nóng chảy, và lại tiếp tục tăng lên.
Quá trình trong hình trên là quá trình nóng chảy của vật .
Vì nhiệt độ của vật ban đầu tăng lên, sau đó nhiệt độ không đổi trong suốt quá trình nóng chảy, và lại tiếp tục tăng lên.