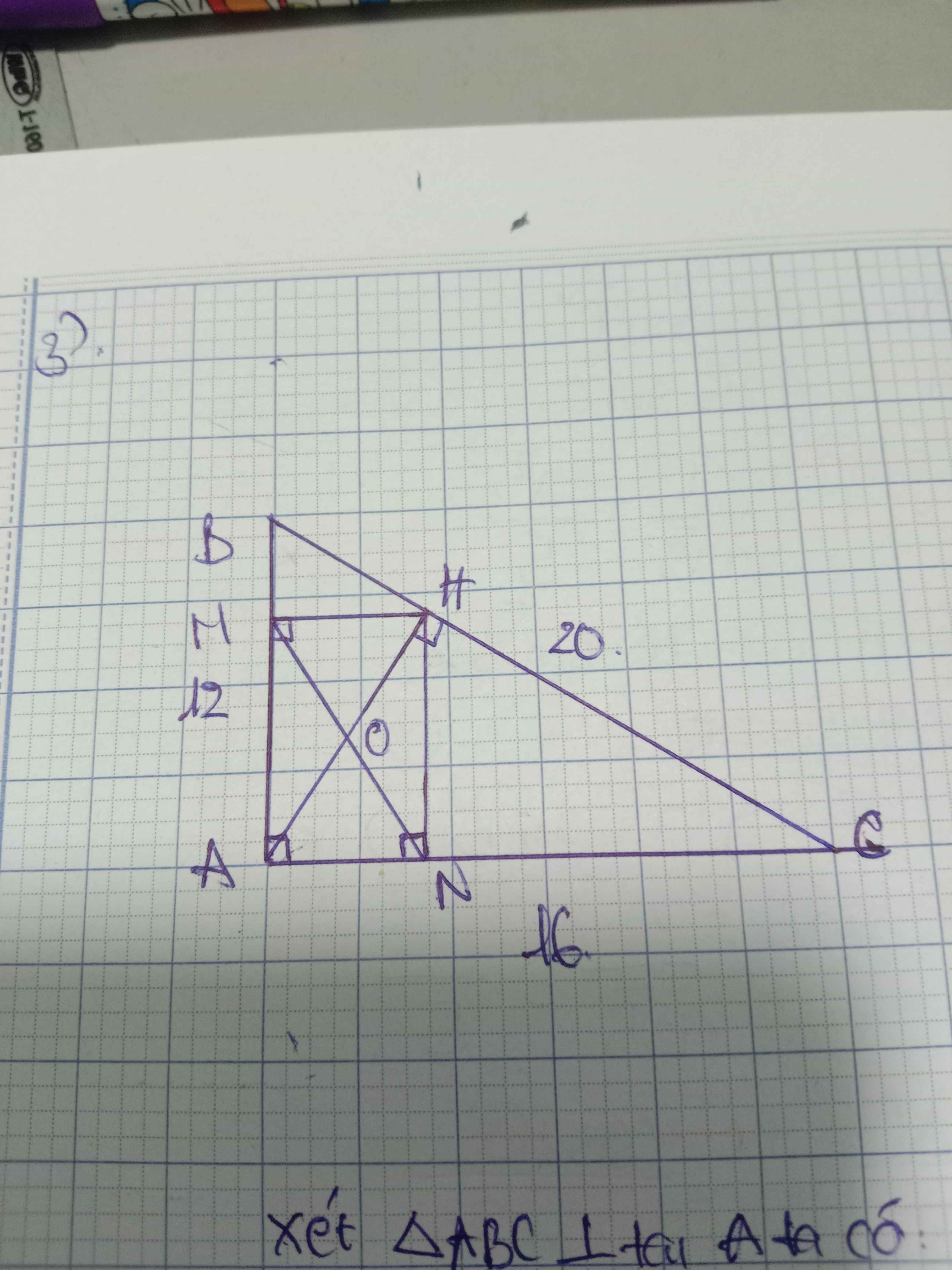
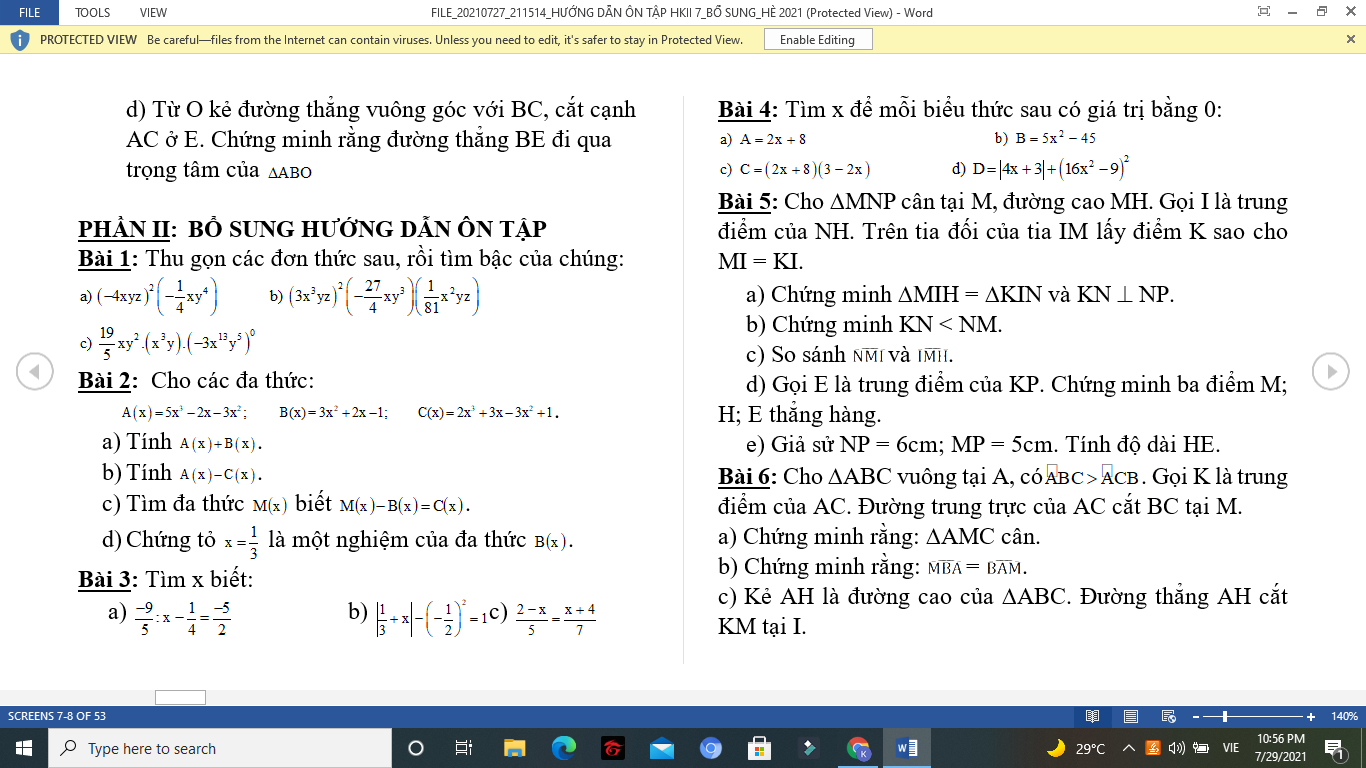
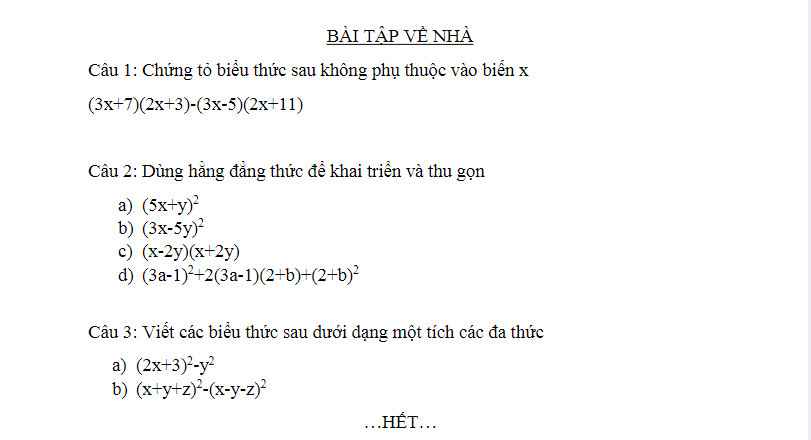giúp em bài D với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 1 2022
d: \(\Leftrightarrow x^2-x-1=x+2\)
\(\Leftrightarrow x^2-2x-3=0\)
=>(x-3)(x+1)=0
=>x=3 hoặc x=-1
e: \(\Leftrightarrow x^2-x-2+x-1=3x+4\)
\(\Leftrightarrow x^2-3-3x-4=0\)
\(\Leftrightarrow x^2-3x-7=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-7\right)=37\)
Vì Δ>0 nên pt có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{37}}{2}\\x_2=\dfrac{3+\sqrt{37}}{2}\end{matrix}\right.\)
1 tháng 9 2021
c: Ta có: \(\tan\widehat{B}+\tan\widehat{C}\)
\(=\dfrac{AB}{AC}+\dfrac{AC}{AB}\)
\(=\dfrac{AB^2}{AC\cdot AB}+\dfrac{AC^2}{AB\cdot AC}\)
\(=\dfrac{BC^2}{AC\cdot AB}\)
\(=\dfrac{BC^2}{AH\cdot BC}=\dfrac{BC}{AH}\)
TP
8 tháng 5 2022
4. \(a.2K+2H_2O\rightarrow2KOH+H_2\\ b.n_K=\dfrac{7,8}{39}=0,2\left(mol\right)\\ n_{H_2}=\dfrac{1}{2}n_K=0,1\left(mol\right)\\ \Rightarrow V_{H_2}=0,1.22,4=2,24\left(l\right)\\ c.n_{KOH}=n_K=0,2\left(mol\right)\\ \Rightarrow m_{KOH}=0,2.56=11,2\left(g\right)\)
Câu d thêm dữ kiện mới tính được em nhé.
VB
1
NT
1
29 tháng 7 2021
Bài 3:
c) Ta có: \(\dfrac{2-x}{5}=\dfrac{x+4}{7}\)
\(\Leftrightarrow14-7x=5x+20\)
\(\Leftrightarrow-7x-5x=20-14\)
\(\Leftrightarrow-12x=6\)
hay \(x=-\dfrac{1}{2}\)
21 tháng 9 2021
\(b,B=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}\left(x\ge0;x\ne4;x\ne9\right)\\ B=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-4+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
\(c,B< A\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}< \dfrac{\sqrt{x}+1}{\sqrt{x}-2}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 0\\ \Leftrightarrow\dfrac{-5}{\sqrt{x}-2}< 0\Leftrightarrow\sqrt{x}-2>0\left(-5< 0\right)\\ \Leftrightarrow x>4\\ d,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{\sqrt{x}-4}{\sqrt{x}+1}=1-\dfrac{5}{\sqrt{x}+1}\in Z\\ \Leftrightarrow5⋮\sqrt{x}+1\Leftrightarrow\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-6;-2;0;4\right\}\\ \Leftrightarrow x\in\left\{0;16\right\}\left(\sqrt{x}\ge0\right)\)
\(e,P=1-\dfrac{5}{\sqrt{x}+1}\)
Ta có \(\sqrt{x}+1\ge1,\forall x\Leftrightarrow\dfrac{5}{\sqrt{x}+1}\ge5\Leftrightarrow1-\dfrac{5}{\sqrt{x}+1}\le-4\)
\(P_{max}=-4\Leftrightarrow x=0\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
Hai câu c và d chỉ là BĐT \(\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\), cách chứng minh \(\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\) thế nào thì chứng minh c và d như vậy (biến đổi thành tổng của 3 bình phương các hiệu)
Với câu c thì \(x=ab;y=bc;z=ca\), câu d thì \(x=a^2b;y=...\)
19 tháng 9 2021
Nhờ thầy viết cho em vài dòng câu d với ạ, câu d em chưa xử lý được thầy ạ?
26 tháng 9 2021
Câu 1:
Ta có: \(\left(3x+7\right)\left(2x+3\right)-\left(3x-5\right)\left(2x+11\right)\)
\(=6x^2+9x+14x+21-\left(6x^2+33x-10x-55\right)\)
\(=6x^2+23x+21-6x^2-23x+55\)
=76