Số giá trị m ∈ Z để phương trình (2sinx -1)(sin2x + 2cosx +m) = 3 - 4cos2x có đúng 2 nghiệm thuộc [0;\(\frac{\pi}{2}\)]
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow\left(cosx+1\right)\left(4cos2x-m.cosx\right)=m\left(1-cosx\right)\left(1+cosx\right)\)
\(\Leftrightarrow4cos2x-m.cosx=m\left(1-cosx\right)\)
\(\Leftrightarrow4cos2x=m\)
\(\Rightarrow cos2x=\dfrac{m}{4}\)
Pt có đúng 2 nghiệm thuộc đoạn đã cho khi và chỉ khi:
\(-1< \dfrac{m}{4}\le-\dfrac{1}{2}\Leftrightarrow-4< m\le-2\)
Có 2 giá trị nguyên của m thỏa mãn

Đáp án B
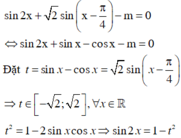
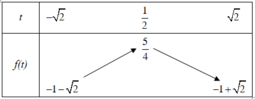
Ta đi tìm m để phương trình 1 − t 2 + t − m = 0 có nghiệm t ∈ − 2 ; 2

Vậy phương trình đã cho có nghiệm ⇔ m = f t có nghiệm trên − 2 ; 2
⇔ m ∈ − 1 − 2 ; 5 4 mà m ∈ ℤ ⇒ m ∈ − 2 ; − 1 ; 0 ; 1
Vậy có 4 giá trị m thỏa mãn.

Đáp án B
sin 2 x + 2 sin x + π 4 − 2 = m ( * ) ⇔ 2 sin x + π 4 2 2 sin x + π 4 = m + 3
Đặt t = 2 sin x + π 4 . Vì x ∈ 0 ; 3 π 4 nên t ∈ 0 ; 2 .
Khi đó phương trình (*) trở thành:
t 2 + t − m − 3 = 0 ( 1 )
Để phương trình (*) có đúng hai nghiệm thuộc khoảng 0 ; 3 π 4 phương trình (1) có đúng một nghiệm thuộc khoảng 0 ; 2
TH1
Δ = 0 0 < − b 2 a < 2 ⇔ 4 m + 4 = 0 0 < − 1 2 < 2 ( V L )
TH2
Δ > 0 f ( 0 ) f ( 2 ) < 0 ⇔ 4 m + 4 > 0 − m − 3 2 − 1 − m < 0 ⇔ m ∈ − 1 ; 2 − 1

Đáp án A
Xét x ∈ - π ; π mà 1 + 2 sin x ≥ 0 1 + 2 cos x ≥ 0 suy ra x ∈ - π 6 ; 2 π 3
Ta có 1 + 2 cos x + 1 + 2 sin x = m 2 ⇔ m 2 8 = 1 + sin x + cos x + 1 + 2 sin x 1 + 2 cos x
Đặt t = sin x + cos x = 2 sin x + π 4 ⇒ t ∈ 3 - 1 2 ; 2 mà 2 sin x . cos x = t 2 - 1 .
Khi đó f t = 1 + t + 2 t 2 + 2 t - 1 , có f ' t = t + 2 t + 1 2 t 2 + 2 t - 1 > 0 , ∀ t ∈ 3 - 1 2 ; 2
Suy ra f(t) là hàm số đồng biến trên 3 - 1 2 ; 2 ⇒ m i n f t = f 2 = 2 + 2 2 m a x f t = f 3 - 1 2 = 1 + 3 2
Do đó, để f t = m 2 8 có nghiệm ⇔ 1 + 3 2 ≤ m 2 8 ≤ 2 + 2 2 ⇔ 2 1 + 3 ≤ m ≤ 4 1 + 2 .
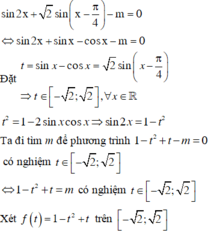

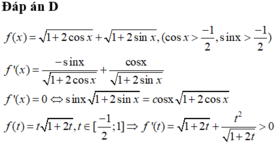
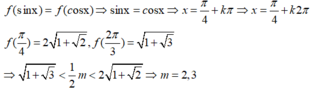
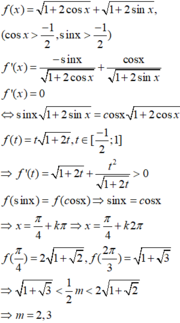
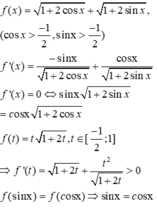
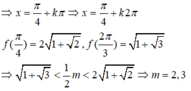


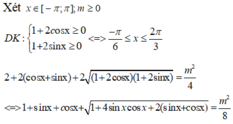
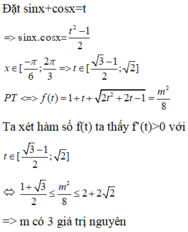
mịnh minhfcoong 4 nhaan7 tám ơ2 l; a ta có số l.5 số là mình có 3 ở mình và 4.6 laf4=7 bà lan .bà thu =5 nhân 4 .hân 9/2 hộc