Bài 2(3 điểm): Giải bài toán bằng cách lập phương trình Một ca nô chạy trên sông trong 8h, xuôi dòng 81 km và ngược dòng 105km. Một lần khác cũng chạy trên khúc sông đó, ca nô này chạy trong 4h, xuôi dòng 54km và ngược dòng 42km. Hãy tính vận tốc khi xuôi dòng và ngược dòng của ca nô, biết vân tốc dòng nước và vận tốc riêng của ca nô không đổi.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 3 2016
gọi x là vận tốc khi xuôi dòng( x>0) (km/h)
gọi y là vận tốc ngược dòng(y>0) (km/h)
*, ca nô chạy trên sông trong 8 giờ:
xuôi dòng 81km:81/x và ngược dòng 105km: 105/y
=> phương trinh: 81/x + 105/y=8 (1)
*,ca nô chạy trong 4 giờ:
xuôi dòng 54km: 54/x và ngược dòng 42km: 42/y
=> ph trình: 54/x + 42/y = 4 (2)
từ (1) và (2) ta có hệ pt:
....
....
..... => x=27km/h
y=21km/h
CM
23 tháng 7 2019
Gọi vận tốc riêng của ca nô và vận tốc dòng nước lần lượt là x, y (km/h; x > y > 0)
Suy ra vận tốc xuôi dòng của ca nô là x + y(km/h); vận tốc ngược dòng là x – y (km/h)
Ca nô chạy trên sông trong 8h xuôi dòng được 81 km và ngược dòng 105 km nên ta có phương trình: 81 x + y + 105 x - y = 8 (1)
Ca nô chạy trên sông trong 4h xuôi dòng được 54km và ngược dòng 42km nên ta có phương trình: 54 x + y + 42 x - y = 4 (2)
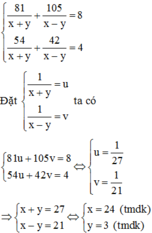
Vậy vận tốc riêng của ca nô và vận tốc dòng nước lần lượt là 24 km/h và 3 km/h
Đáp án: D
T
13 tháng 4 2020
Gọi x (km/h) là vận tốc riêng của cano.(x>0)
Gọi y (km/h) là vận tốc dòng nước.(y>0)
Theo đề bài ta có hệ phương trình:
\(\hept{\begin{cases}\frac{81}{x+y}+\frac{105}{x-y}=8\\\frac{54}{x+y}+\frac{42}{x-y}=4\end{cases}}\)
Giải ra ta được:
\(\hept{\begin{cases}x+y=27\\x-y=21\end{cases}\Leftrightarrow\hept{\begin{cases}x=24\\y=3\end{cases}}}\)
Vậy vận tốc riêng của cano là 24km/h.
Vận tốc dòng nước là 3km/h
6 tháng 6 2021
gọi vận tốc ca nô xuôi dòng là x+y(km/h)(x>0)
vận tốc ca nô ngược dòng là :x-y(km/h)(y>0)(x>y)
ta có hệ pt: \(\left\{{}\begin{matrix}\dfrac{60}{x+y}+\dfrac{48}{x-y}=6\\\dfrac{40}{x+y}+\dfrac{80}{x-y}=7\end{matrix}\right.\)
giải hệ pt trên bằng cách đặt\(\dfrac{1}{x+y}=a\) và \(\dfrac{1}{x-y}=b\)
=>\(\left\{{}\begin{matrix}60a+48b=6\\40a+80b=7\end{matrix}\right.\) giải hệ pt này =>\(\left\{{}\begin{matrix}a=\dfrac{1}{20}\\b=\dfrac{1}{16}\end{matrix}\right.\)=>\(\left\{{}\begin{matrix}\dfrac{1}{x+y}=\dfrac{1}{20}\\\dfrac{1}{x-y}=\dfrac{1}{16}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+y=20\\x-y=16\end{matrix}\right.< =>\left\{{}\begin{matrix}x=18\left(TM\right)\\y=2\left(TM\right)\end{matrix}\right.\)
vậy vận tốc riêng ca nô là 18km/h , vận tốc dòng nước là 2km/h
AH
Akai Haruma
Giáo viên
9 tháng 6 2021
Lời giải:
Gọi vận tốc xuôi dòng là $a$ (km/h) và vận tốc ngược dòng là $b$ (km/h)
Theo bài ra ta có:
\(\left\{\begin{matrix} \frac{96}{a}+\frac{48}{b}=5\\ \frac{48}{a}+\frac{60}{b}=4\end{matrix}\right.\Rightarrow \left\{\begin{matrix} \frac{1}{a}=\frac{1}{32}\\ \frac{1}{b}=\frac{1}{24}\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} a=32\\ b=24\end{matrix}\right.\) (km/h)
Vận tốc riêng của cano: $(32+24):2=28$ (km/h)
Vận tốc dòng nước: $32-28=4$ (km/h)
10 tháng 6 2019
gọi vận tốc thật là V, vận tốc dòng là v
=> vận tốc khi đi xuôi dòng là V+v
vận tốc khi đi ng­­ược dòng là V-v
lần đi 1 có tổng thời gian là 7 h ,xuôi dòng 108km ,ngược dòng 63km=>
108V+v+63V−v=7(1)
lần 2 có tổng thời gian là 7 h , xuôi dòng 81km, ngược dòng 84km=>
81V+v+84V−v=7(2)
kết hợp (1) và (2) ta được hệ PT 2 ẩn
quy đồng lên giải dễ dàng
T
10 tháng 6 2019
#)Giải :
Gọi x (km/h) là vận tốc của dòng nước
y (km/h) là vận tốc riêng của cano. đk: x, y > 0.
vân tốc khi xuối dòng : y + x
vận tốc khi ngược dòng : y - x
*108 / (y + x) + 63 / (y - x) = 7
* 81 / (y + x) + 84 / (y - x) = 7
có thể quy đồng và giải trực tiếp hệ trên. tuy nhiên nếu đặt ẩn phụ thì nhẹ hơn:
đặt u = 1/(y + x); v = 1/(y - x).
ta có hệ pt:
108u + 63v = 7
81u + 84v = 7
=> u =1/27 ; v = 1/21
=> ta có hệ pt:
y + x = 1/u = 27
y - x = 1/v = 21
=> x = 3 km/h; y = 24 km/h
TM
6 tháng 3 2023
Gọi \(a,b\) lần lượt là vận tốc riêng của ca nô và vận tốc dòng nước \(\left(a>b>0\right)\).
Thời gian ca nô đi xuôi dòng khúc sông \(60km\) là : \(\dfrac{60}{a+b}\left(h\right)\).
Thời gian ca nô đi ngược dòng \(48km\) là : \(\dfrac{48}{a-b}\left(h\right)\).
Theo đề bài thì \(\dfrac{60}{a+b}+\dfrac{48}{a-b}=6\left(1\right)\).
Thời gian ca nô đi xuôi dòng \(40km\) là : \(\dfrac{40}{a+b}\left(h\right)\).
Thời gian ca nô đi ngược dòng \(80km\) là : \(\dfrac{80}{a-b}\left(h\right)\)
Cũng theo đề bài, ta có : \(\dfrac{40}{a+b}+\dfrac{80}{a-b}=7\left(2\right)\).
Từ \((1)\) và \((2)\), ta có hệ phương trình :
\(\left\{{}\begin{matrix}\dfrac{60}{a+b}+\dfrac{48}{a-b}=6\\\dfrac{40}{a+b}+\dfrac{80}{a-b}=7\end{matrix}\right.\left(I\right)\)
Đặt : \(x=\dfrac{20}{a+b}\) và \(y=\dfrac{16}{a-b}\). Hệ \((I)\) được viết lại thành :
\(\left\{{}\begin{matrix}3x+3y=6\\2x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=2\\2x+5y=7\end{matrix}\right.\)
Hay : \(\left\{{}\begin{matrix}5x+5y=10\\2x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=3\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{20}{a+b}=1\\\dfrac{16}{a-b}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=20\\a-b=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=36\\a+b=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=18\\b=2\end{matrix}\right.\) (thỏa mãn).
Vậy : Vận tốc riêng của ca nô là \(18(km/h)\) và vận tốc dòng nước là \(2(km/h).\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2023
Gọi vận tốc riêng của cano là x (km/h) với x>0
Gọi vận tốc của dòng nước là y (km/h) với y>0 và y<x
Vận tốc cano khi xuôi dòng: \(x+y\) (km/h)
Vận tốc cano khi ngược dòng: \(x-y\) (km/h)
Do cano xuôi dòng 60km và ngược dòng 48km hết 6h nên ta có:
\(\dfrac{60}{x+y}+\dfrac{48}{x-y}=6\)
Do cano xuôi dòng 40km và ngược dòng 80km thì hết 7h nên ta có:
\(\dfrac{40}{x+y}+\dfrac{80}{x-y}=7\)
Ta được hệ: \(\left\{{}\begin{matrix}\dfrac{60}{x+y}+\dfrac{48}{x-y}=6\\\dfrac{40}{x+y}+\dfrac{80}{x-y}=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{120}{x+y}+\dfrac{96}{x-y}=12\\\dfrac{120}{x+y}+\dfrac{240}{x-y}=21\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{120}{x+y}+\dfrac{96}{x-y}=12\\\dfrac{144}{x-y}=9\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x-y=16\\\dfrac{120}{x+y}+\dfrac{96}{16}=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x-y=16\\x+y=20\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=18\\y=2\end{matrix}\right.\)
14 tháng 3 2022
Gọi vận tốc thực của ca nô là \(x\left(km/h\right)\)dòng nước là \(y\left(km/h\right)\)với \(x>y>0\)
Vận tốc xuôi dòng là \(x+y\left(km/h\right)\), vận tốc ngược dòng là \(x-y\left(km/h\right)\)
Lần đi thứ nhất, thời gian ca nô đi xuôi dòng là: \(\frac{70}{x+y}\left(h\right)\), thời gian ca nô đi ngược dòng là \(\frac{50}{x-y}\left(h\right)\)
Lần đi thứ hai, thời gian ca nô đi xuôi dòng là: \(\frac{35}{x+y}\left(h\right)\), thời gian ca nô đi ngược dòng là \(\frac{75}{x-y}\left(h\right)\)
Vì lần thứ nhất, ca nô dành ra 4h để đi xuôi và ngược dòng nên ta có pt \(\frac{70}{x+y}+\frac{50}{x-y}=4\)(1)
Lần thứ hai, ca nô cũng dành ra 4h để đi xuôi và ngược dòng nên ta có pt \(\frac{35}{x+y}+\frac{75}{x-y}=4\)(2)
Từ (1) và (2) ta có hpt \(\hept{\begin{cases}\frac{70}{x+y}+\frac{50}{x-y}=4\\\frac{35}{x+y}+\frac{75}{x-y}=4\end{cases}}\)(*)
Đặt \(\hept{\begin{cases}\frac{35}{x+y}=a\left(a>0\right)\\\frac{25}{x-y}=b\left(b>0\right)\end{cases}}\), khi đó (*) trở thành \(\hept{\begin{cases}2a+2b=4\\a+3b=4\end{cases}}\Leftrightarrow\hept{\begin{cases}a+b=2\\a+3b=4\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=1\end{cases}}\)(nhận)
\(\Rightarrow\hept{\begin{cases}\frac{35}{x+y}=1\\\frac{25}{x-y}=1\end{cases}}\Rightarrow\hept{\begin{cases}x+y=35\\x-y=25\end{cases}}\Leftrightarrow\hept{\begin{cases}x=30\\y=5\end{cases}}\)(nhận)
Vậy vận tốc dòng nước là \(5km/h\)