cho hai đường thẳng AA' và BB' cắt nhau tại điểm C. Biết ACB + A'CB'=60 độ. Tính ACB,BCA'.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 5 2018
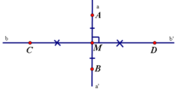
Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.
CM
9 tháng 6 2018
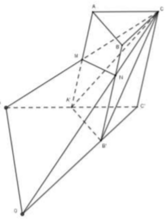
Sử dụng công thức tính thể tích khối chóp V = 1 3 h . S với h là chiều cao hình chóp và S là diện tích đáy.
Công thức tính thể tích lăng trụ V = h.S với h là chiều cao hìnhlăng trụ và S là diện tích đáy.
Cách giải:
6 tháng 8 2021
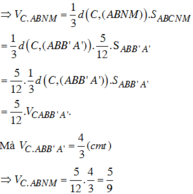
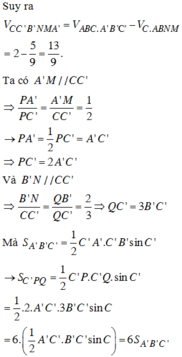
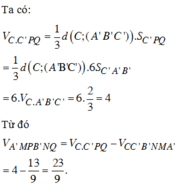
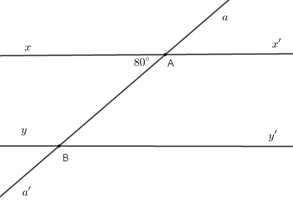
a'a không song song với b'b
Vì ở vị trí đồng vị cMa ko bằng MNb
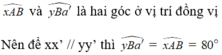
Có : \(\widehat{ACB}+\widehat{A'CB'}=60^0\)
Mà \(\widehat{ACB}=\widehat{A'CB'}\) (2 góc đối đỉnh )
=>\(\widehat{ACB}=\widehat{A'CB'}=\dfrac{60}{2}=30^0\)
Ta có \(\widehat{ACB}+\widehat{BCA'}=180^0\) (2 góc kề bù )
=> \(\widehat{BCA'}=180^0-\widehat{ACB}=180^0-30^0=150^0\)