Câu 1: Cho ba điểm \(A\left(2;0\right);B\left(0;-2\right);C\left(3;1\right)\)
a, Viết phương trình đường thẳng AB
b, Chứng minh: A; B; C thẳng hàng
Giải giúp mk vs ạ!!!!! thanks m.n nhìu nà !?!!?!!!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
1
Những câu hỏi liên quan
21 tháng 2 2021
Đáp án:
AD+BC
=ED-EA+EC-EB
=(ED+EC)-(EA+EB) (1)
Mà E là trung điểm của AB=> EA+EB=0
(1)=2EF (F là trung điểm DC)
4 tháng 1
E trên trục hoành nên E(x;0)
A(6;3); B(-3;6); E(x;0)
\(\overrightarrow{AB}=\left(-9;3\right);\overrightarrow{AE}=\left(x-6;-3\right)\)
Để A,B,E thẳng hàng thì \(\dfrac{x-6}{-9}=\dfrac{-3}{3}=-1\)
=>x-6=9
=>x=15
Vậy: E(15;0)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1
Do E thuộc trục hoành nên tọa độ có dạng \(E\left(x;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-9;3\right)\\\overrightarrow{AE}=\left(x-6;-3\right)\end{matrix}\right.\)
3 điểm A, B, E thẳng hàng khi:
\(\dfrac{x-6}{-9}=\dfrac{-3}{3}\Rightarrow x-6=9\)
\(\Rightarrow x=15\Rightarrow E\left(15;0\right)\)
5 tháng 1 2020
Goi 3 canh cua tam giac la a,b,c . Goi a bang x
ta co :
4a/2=12b/2=xc/2=S
suy ra a=2 ; b=6 ; 2S/x. Do x-y [bat dang thuc trong tam giac]
suy ra S/2-S/6<2S ma x<2S/3.Ma x thuoc Z
suy ra x=4,5
5 tháng 1 2020
{CAU 2 } xet thay h 4 so la so am
suy ra co 1 hoac 3 so la so am trong h do
xet tung truong hop ta co:
+ co 1 so am
[x mu 2] - 10< [x mu 2] -7 suy ra [x mu 2] - 10 <0 < [x mu hai] -7
suy ra 7<[x mu2]<10 suy ra [x mu 2] = 9 suy ra x= 3 hoac -3
+co 3 so am 1 so duong
[x mu 2] - 4<[x mu 2 ] -1 <[ x mu 2] <4
suy ra khong co gia tri thoa man
Vay x=3;-3
21 tháng 5 2023
Câu 2: pt đã cho \(\Leftrightarrow x^3-3x^2+3x-1+x^3+x^3+3x^2+3x+1=x^3+6x^2+12x+8\)
\(\Leftrightarrow2x^3-6x^2-6x-8=0\)
\(\Leftrightarrow x^2-3x^2-3x-4=0\)
\(\Leftrightarrow\left(x-1\right)^3-6\left(x-1\right)-9=0\) (*)
Đặt \(x-1=t\) thì (*) trở thành \(t^3-6t-9=0\)
\(\Leftrightarrow t^3-9t+3t-9=0\)
\(\Leftrightarrow t\left(t^2-9\right)+3\left(t-3\right)=0\)
\(\Leftrightarrow\left(t-3\right)\left(t^2+3t\right)+3\left(t-3\right)=0\)
\(\Leftrightarrow\left(t-3\right)\left(t^3+3t+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=3\\t^2+3t+3=0\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow x-1=3\)
\(\Leftrightarrow x=4\)
Vậy pt đã cho có nghiệm \(x=4\)
21 tháng 5 2023
bài đấy thì em làm được rồi á. Chỉ là em đăng lên xem còn cách nào giải hay hơn thôi ạ...
19 tháng 12 2023
Câu 1:
\(A=\left(2\sqrt{3}+4\cdot\sqrt{27}-\sqrt{108}\right):2\sqrt{3}\)
\(=\dfrac{\left(2\sqrt{3}+4\cdot3\sqrt{3}-6\sqrt{3}\right)}{2\sqrt{3}}\)
\(=\dfrac{2\sqrt{3}+12\sqrt{3}-6\sqrt{3}}{2\sqrt{3}}=\dfrac{8\sqrt{3}}{2\sqrt{3}}=4\)
\(B=\sqrt{9+4\sqrt{5}}-2\left(\sqrt{5}+1\right)\)
\(=\sqrt{5+2\cdot\sqrt{5}\cdot2+4}-2\left(\sqrt{5}+1\right)\)
\(=\sqrt{\left(\sqrt{5}+2\right)^2}-2\left(\sqrt{5}+1\right)\)
\(=\sqrt{5}+2-2\sqrt{5}-2=-\sqrt{5}\)
Câu 2:
a: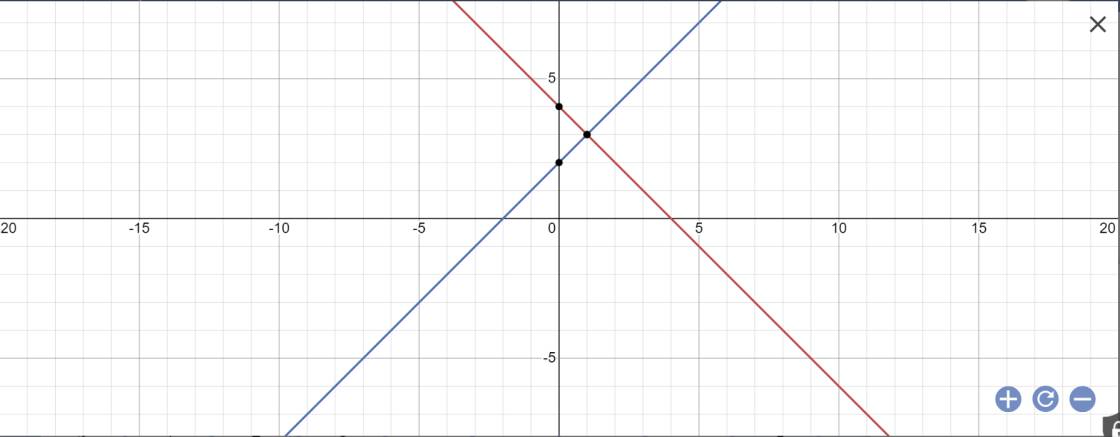 
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(m\cdot1+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)
Câu 4:
a: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
Xét tứ giác CMON có \(\widehat{CMO}=\widehat{CNO}=\widehat{MCN}=90^0\)
=>CMON là hình chữ nhật
b: Ta có: ΔCAB vuông tại C
=>CA\(\perp\)CB tại C
=>AC\(\perp\)EB tại C
Xét ΔAEB vuông tại A có AC là đường cao
nên \(EC\cdot CB=AC^2\left(1\right)\)
Xét ΔCAB vuông tại C có CH là đường cao
nên \(AH\cdot AB=AC^2\left(2\right)\)
Từ (1) và (2) suy ra \(EC\cdot CB=AH\cdot AB\)
c: Ta có: ΔOAC cân tại O
mà OM là đường cao
nên OM là phân giác của góc AOC
Xét ΔOAI và ΔOCI có
OA=OC
\(\widehat{AOI}=\widehat{COI}\)
OI chung
Do đó: ΔOAI=ΔOCI
=>\(\widehat{OAI}=\widehat{OCI}=90^0\)
Ta có: ΔOBC cân tại O
mà ON là đường cao
nên ON là phân giác của góc COB
Xét ΔOBF và ΔOCF có
OB=OC
\(\widehat{BOF}=\widehat{COF}\)
OF chung
Do đó: ΔOBF=ΔOCF
=>\(\widehat{OBF}=\widehat{OCF}=90^0\)
Ta có: \(\widehat{ICF}=\widehat{ICO}+\widehat{FCO}\)
\(=90^0+90^0=180^0\)
=>I,C,F thẳng hàng
=>OC\(\perp\)IF tại C
Xét (O) có
OC là bán kính
IF\(\perp\)OC tại O
Do đó: IF là tiếp tuyến của (O)
10 tháng 2 2021
\(\overrightarrow{AB}=\left(4;4\right);\overrightarrow{AE}=\left(a+1;b+2\right)\) mà E di động trên đường thẳng AB nên A,B,E thẳng hàng tương đương với \(\dfrac{a+1}{4}=\dfrac{b+2}{4}\) <=> \(a=b+1\).Vậy E(b+1;b)
Đặt \(\overrightarrow{u}=2\overrightarrow{EA}+3\overrightarrow{EB}-\overrightarrow{EC}\) => \(\overrightarrow{u}=\left(-1-4b;3-4b\right)\)
có : \(\left|2\overrightarrow{EA}+3\overrightarrow{EB}-\overrightarrow{EC}\right|=\left|\overrightarrow{u}\right|=\sqrt{\left(-1-4b\right)^2+\left(3-4b^2\right)}\)
Đặt : 1-4b = t => \(\left\{{}\begin{matrix}-1-4b=t-2\\3-4b=t+2\end{matrix}\right.\) khi đó \(\left|\overrightarrow{u}\right|=\sqrt{\left(t-2\right)^2+\left(t+2\right)^2}=\sqrt{2t^2+8}\ge2\sqrt{2}\)
\(\left|2\overrightarrow{EA}+3\overrightarrow{EB}-\overrightarrow{EC}\right|\)đạt GTNN khi và chỉ khi t =0 <=> b=1/4 => a=5/4
vậy \(a^2-b^2=\dfrac{3}{2}\)
a/ Gọi phương trình đường thẳng cần tìm có dạng: y = ax + b
Vì đường thẳng đi qua A,B nên ta có hệ
\(\hept{\begin{cases}0=2a+b\\-2=b\end{cases}\Leftrightarrow\hept{\begin{cases}a=1\\b=-2\end{cases}}}\)
Vậy phương trình đường thẳng AB là:
\(y=x-2\)
b/ Ta chứng minh C thuộc đường AB
Ta thế tọa độ điểm C vào đường thẳng AB thì được
\(1=3-2\)(đúng)
Vậy C thuộc đường thẳng AB hay A,B,C thẳng hàng