cho △ ABC cân tại A , vẽ đường trung tuyến AM
a, chứng minh △ ABM=tam giác ACM
b, chứng minh AM vuông góc BC
c, tính AM biết AB=5cm , BC=6cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

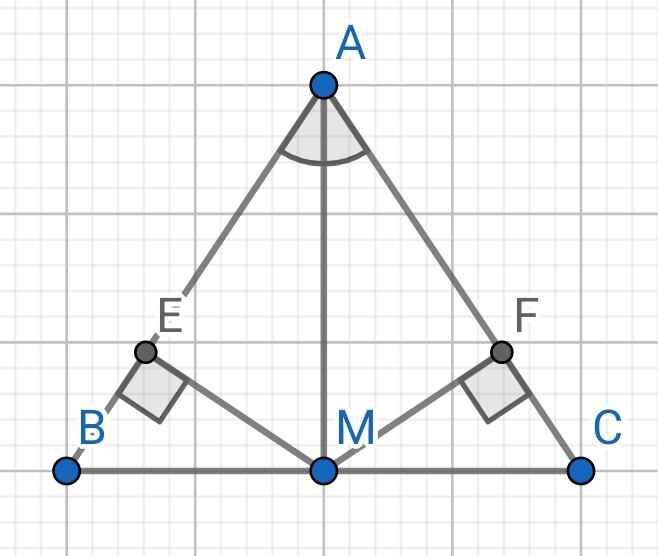 a) Do AM là tia phân giác của ∠BAC (gt)
a) Do AM là tia phân giác của ∠BAC (gt)
⇒ ∠BAM = ∠CAM
Xét ∆ABM và ∆ACM có:
AB = AC (gt)
∠BAM = ∠CAM (cmt)
AM là cạnh chung
⇒ ∆ABM = ∆ACM (c-g-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ BM = CM (hai cạnh tương ứng)
⇒ M là trung điểm của BC
Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
c) Do ∠BAM = ∠CAM (cmt)
⇒ ∠EAM = ∠FAM
Xét hai tam giác vuông: ∆AME và ∆AMF có:
AM là cạnh chung
∠EAM = ∠FAM (cmt)
⇒ ∆AME = ∆AMF (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng)
a,
Xét tam giác ABC có:
+ AB = AC (giả thuyết)
+ Góc CAM = MAB (AM là phân giác góc BAC)
+ AM chung
⇒ 2 tam giác bằng nhau (cgc) (đpcm)
b,
Ta có:
+ Tam giác AMC = Tam giác ABM (theo câu a)
⇒ CM = MB (2 cạnh tương ứng) (1)
⇒ M là trung điểm BC (đpcm)
+ Mà AM là tia phân giác góc CAB (2)
+ Góc AMC = Góc AMB (3)
Từ (1), (2), (3).
⇒ AM ⊥ BC (t/c) (đpcm)
c,
Ta có:
Tam giác ACM = Tam giác ABM (theo câu A)
⇒ Góc ACM = Góc ABM (2 góc tương ứng)
Ta có:
+ ME ⊥ AB (giả thuyết)
⇒ Tam giác MEB vuông tại E
+ MF ⊥ AC (giả thuyết)
⇒ Tam giác CFM vuông tại F
Xét tam giác CFM vuông tại F và tam giác MEB vuông tại E có:
+ Góc ACM bằng góc ABM (chứng minh trên)
+ MC = MB (theo câu b)
⇒ Hai tam giác CFM = MEB (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng) (đpcm)

Cho △ABC có AB = AC, AM là phân giác của ∠BAC (M ∈ BC):
a, Chứng minh △ABM = △ACM.
b, Chứng minh M là trung điểm của BC và AM ⊥ BC.
c, Kẻ MF ⊥ AB (F ∈ AB) và ME ⊥ AC (E ∈ AC). Chứng minh EF // BC.
Giải:
a,
- Xét 2 △ABM và △ACM, có:
AB = AC (theo giả thiết)
∠CAM = ∠BAM (AM là phân giác của ∠BAC)
AM_cạnh chung
=> △ABM = △ACM (c.g.c)
b,
- Có △ABM = △ACM (chứng minh trên)
=> MC = MB (2 cạnh tương ứng)
=> M là trung điểm của BC
=> ∠AMC = ∠AMB (2 góc tương ứng)
mà 2 ∠AMC và ∠AMB kề bù
=> ∠AMC = ∠AMB = \(\dfrac{180^o}{2}\) = 90o
<=> AM ⊥ BC
c,
- Xét 2 △AEM và △AFM, có:
∠AEM = ∠AFM = 90o
AM_cạnh chung
∠EAM = ∠FAM (AM là phân giác của ∠EAF)
=> △AEM = △AFM (cạnh huyền - góc nhọn)
=> AE = AF (2 cạnh tương ứng)
<=> △AEF cân tại A
=> ∠AEF = \(\dfrac{180^o-\text{∠}EAF}{2}\) (số đo của một góc ở đáy trong △AEF cân tại A) (1)
Có △ABC cân tại A (AB = AC)
=> ∠ACB = \(\dfrac{180^o-\text{∠}BAC}{2}\) (số đo của một góc ở đáy trong ΔABC cân tại A) (2)
Từ (1) và (2) suy ra ∠AEF = ∠ACB
mà ∠AEF và ∠ACB ở vị trí đồng vị
=> EF//BC

a: Xét ΔABM và ΔACM có
AB=AC
BM=Cm
AM chung
=>ΔABM=ΔACM
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
c: BM=CM=5cm
=>AM=12cm
=>AG=8cm

a) Xét ΔABC có AB=AC=5
=> ΔABC cân tại A
ta có AM là trung tuyến => AM là đường phân giác của góc A (tc Δ cân)
=>\(\widehat{B}=\widehat{C}\)(tc)
Xét ΔABM và ΔACM có
AB=AC gt
có AM là trung tuyến => BM=CM
\(\widehat{B}=\widehat{C}\) (cmt)
=>ΔABM = ΔACM (cgc)
b) có ΔABC cân
mà AM là trung tuyến => AM là đường cao (tc Δ cân)
c) ta có AM là trung tuyến =>
M là trung điểm của BC
=> BM=CM=\(\dfrac{BC}{2}=\dfrac{6}{2}=3\)cm
Xét ΔABM có AM là đường cao => \(\widehat{AMB}=\)90o
=> AM2+BM2=AB2
=> AM2+32=52
=> AM =4 cm
d) Xét ΔBME và ΔCMF có
\(\widehat{MEB}=\widehat{MFC}=\)90o (ME⊥AB,MF⊥AC)
BM=CM (cmt)
\(\widehat{B}=\widehat{C}\)
=>ΔBME = ΔCMF (ch-cgv)
=>EM=FM( 2 góc tương ứng)
Xét ΔMEF có
EM=FM (cmt)
=> ΔMEF cân tại M

mình chỉ giúp ý d theo mong muốn của bạn thôi :)
Có : AH = AK ( cái này bạn chứng minh ở câu trên chưa mình không biết; nếu chưa thì bạn chứng minh đi nhé )
=> A thuộc đường trung trực của HK
và MH=MK
=> M thuộc đường trung trực của HK
=> AM là đường trung tực của HK
=> AM ⊥ HK

a: Xét ΔAKM vuông tại K và ΔANM vuông tại N có
AM chung
góc KAM=góc NAM
=>ΔAKM=ΔANM
=>MK=MN
b: BM=CM=3cm
AM=căn 5^2-3^2=4cm
c; AK=AN
MK=MN
=>AM là trung trực của KN
=>AM vuông góc KN



Dễ và cơ bản mà nhỉ:vv
a) Xét ∆ABM và ∆ACM:
AB=AC (∆ABC cân tại A)
BM=CM (AM là trung tuyến)
\(\widehat{ABM}=\widehat{ACM}\) (∆ABC cân tại A)
=> ∆ABM=∆ACM (c.g.c)
b) Theo câu a: ∆ABM=∆ACM
=> \(\widehat{AMB}=\widehat{AMC}\)
Mà \(\widehat{AMB}+\widehat{AMC}=180^o\) (2 góc kề bù)
=> \(\widehat{AMB}=\widehat{AMC}=90^o\)
=> AM vuông góc với BC
c) M là trung điểm của BC
=> \(MB=MC=\dfrac{BC}{2}=\dfrac{6}{2}=3\)
Áp dụng định lý Py-ta-go vào ∆ABM, ta có:
\(AB^2=AM^2+BM^2\)
\(\Leftrightarrow5^2=AM^2+3^2\Rightarrow AM^2=5^2-3^2=16=4^2\)
\(\Rightarrow AM=4\) (cm)
Vậy AM=4cm.
b) Cm theo cách khác:
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MB=MC(M là trung điểm của BC)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của BC
hay AM\(\perp\)BC(đpcm)