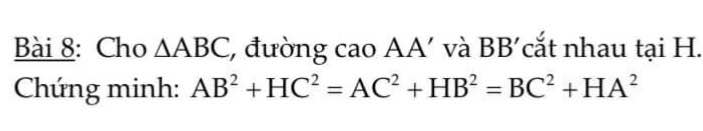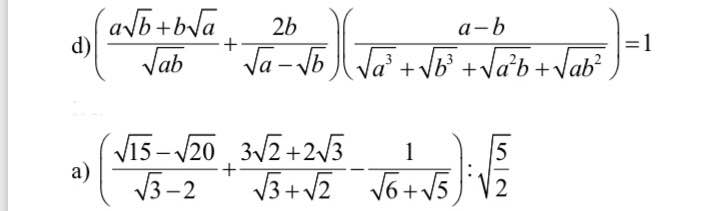Giải giúp mình với. Cảm ơn nhiều!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
giải giúp mình với mình cảm ơn nhiều
N
0
giải giúp mình với, cảm ơn nhiều
9 tháng 4 2021
a) Xét tứ giác ADHE có
\(\widehat{ADH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{ADH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADHE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
9 tháng 4 2021
a) Xét tứ giác BDEC có
\(\widehat{BDC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BDC}\) và \(\widehat{BEC}\) là hai góc cùng nhìn cạnh BC
Do đó: BDEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
N
0
AT
16 tháng 7 2021
Ta có: \(AB^2+HC^2=\left(AA'^2+A'B^2\right)+\left(A'H^2+A'C^2\right)\)
\(=\left(AA'^2+A'C^2\right)+\left(A'B^2+A'H^2\right)=AC^2+HB^2\)
Lại có: \(BC^2+HA^2=\left(BB'^2+B'C^2\right)+\left(B'H^2+B'A^2\right)\)
\(=\left(BB'^2+B'A^2\right)+\left(B'C^2+B'H^2\right)=AB^2+HC^2\)
\(\Rightarrow AB^2+HC^2=AC^2+HB^2=BC^2+HA^2\)
28 tháng 7 2021
d) Ta có: \(\left(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}+\dfrac{2b}{\sqrt{a}-\sqrt{b}}\right)\left(\dfrac{a-b}{\sqrt{a^3}+\sqrt{b^3}+\sqrt{a^2b}+\sqrt{ab^2}}\right)\)
\(=\left(\sqrt{a}+\sqrt{b}+\dfrac{2b}{\sqrt{a}-\sqrt{b}}\right)\cdot\left(\dfrac{a-b}{a\sqrt{a}+b\sqrt{b}+a\sqrt{b}+b\sqrt{a}}\right)\)
\(=\dfrac{a-b+2b}{\sqrt{a}-\sqrt{b}}\cdot\dfrac{a-b}{\left(\sqrt{a}+\sqrt{b}\right)\left(a+b\right)}\)
\(=\dfrac{\left(a+b\right)\cdot\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\left(a+b\right)\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
=1
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 6 2021
\(\Leftrightarrow16x^4-4x^2-4xy+y^2+1=0\)
\(\Leftrightarrow\left(16x^4-8x^2+1\right)+\left(4x^2-4xy+y^2\right)=0\)
\(\Leftrightarrow\left(4x^2-1\right)^2+\left(2x-y\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x^2-1=0\\2x-y=0\end{matrix}\right.\)
\(\Leftrightarrow\left(x;y\right)=\left(-\dfrac{1}{2};-1\right);\left(\dfrac{1}{2};1\right)\)