Cho tam giác ABC có diện tích là 16cm2. Gọi D, E lần lượt là trung điểm của các cạnh AB, AC. Tính diện tích tam giác ADE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 12 2019
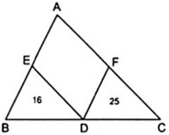
Đặt S A B C = S . Vì DE//AC nên Δ BED ∼ Δ BAC
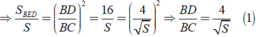
Lại có DF//AB nên Δ CDF ∼ Δ CBA
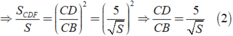
Cộng theo vế của đẳng thức ( 1 ) và ( 2 ) ta được:
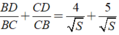
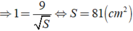
Vậy diện tích của tam giác ABC là 81 c m 2
6 tháng 1 2018
Nối D với C
Ta có: diện tích ADE = diện tích DCB (vì chung đường cao hạ từ C, DA=DB)
<=> diện tích ADC = 72 :2 = 36 (cm vuông)
Ta lại có diện tích ADE bằng diện tích DEC ( vì chung đường cao hạ từ D, EA = EC)
<=> diện tích ADE =36:2= 18 (cm vuông)
6 tháng 1
Ta có:
\(S_{AGD}=S_{DEG}=S_{GEC}=S_{EDB}\)
Nên:
\(S_{DEG}=\dfrac{ABC}{4}=\dfrac{100}{4}=25\left(m^2\right)\)
Đ/S:....
8 tháng 1 2019
Nhận xét : AEB và EBC có cùng chiều cao và độ dài đáy
Mà SAEB = SEBC = 72 : 2 = 36cm2
Vậy SADE = SDEB = 36 : 2 = 18cm2
Đáp số :
13 tháng 12 2015
Nối E với B
Xét hai tam giác ABE và ABC
- Chùng chiều cao hạ từ đỉnh B xuống AC
- AE = 1/2AC
=> SABE = SABC x 1/2 = 360 x 1/2 = 180 ( cm2 )
Xét hai tam giác ADE và ABE
- Chung chiều cao hạ từ đỉnh E xuống AB
- AD = 1/2 AB
=> SADE = SABE x 1/2 = 180 x 1/2 = 90 ( cm2 )
Đáp số : 90 cm2