Question

[Tung Nguyễn Đình]

Một lăng kính có góc chiết quang A, chiết suất n= 3 . Chiếu một tia tới, nằm trong một tiết diện thẳng
vào một mặt bên sao cho góc lệch của tia l

ó so với tia tới là cực tiểu và bằng A. Hãy chọn câu trả lời đúng khi nói
về giá trị của góc tới i và góc lệch D:
A. i=45o, D=60o. B. i=60o, D=45o.` C. i=45o, D=45o. D. Cả A, B và C đều sai.

Answer 1

[Đào Tùng Dương]

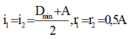
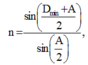
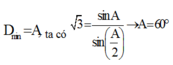
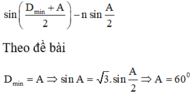
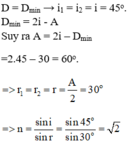
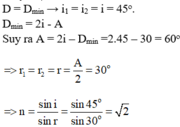
Góc lệch giữa tia tia tới và tia ló cực tiểu :

\(D_{min}\Leftrightarrow i_1=i_2;D_{min}=2i_1-\widehat{A}\)

\(n=\dfrac{sin\left(\dfrac{D_{min}+A}{2}\right)}{sin\dfrac{A}{2}}\Leftrightarrow\)

\(B:i=45^o;D=60^o\Rightarrow D_{min}=75^o\)

\(\Rightarrow\dfrac{sin\left(\dfrac{75^o+45^o}{2}\right)}{sin\dfrac{45}{2}}=2,263\ne\sqrt{3}\Leftrightarrow B.sai\)

\(A:i=45^o;D=60^o\Rightarrow D_{min}=30^o\)

\(\Rightarrow\dfrac{sin\left(\dfrac{30^o+60^o}{2}\right)}{sin\dfrac{60}{2}}=\sqrt{2}\ne\sqrt{3}\Leftrightarrow A.sai\)

\(C:i=45^o;D=45^o\Rightarrow D_{min}=45^o\)

\(\Rightarrow\dfrac{sin\left(\dfrac{45^o+45^o}{2}\right)}{sin\dfrac{45^o}{2}}=1,84776\ne\sqrt{3}\Rightarrow C.sai\)

=> Chọn D