tìm m để phươg trình x2 - 2(2m+1)x+4m2 +4m=0 có hai nghiệm phân biệt x1,x2.
chứng minh rằng: (x12-4mx1+4m2)(x22-4mx2+4m2)=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
3 log 27 2 x 2 - x + 2 m - 4 m 2 + log 1 3 x 2 + m x - 2 m 2 = 0 ⇔ log 3 2 x 2 - x + 2 m - 4 m 2 = log 3 x 2 + m x - 2 m 2 ⇔ x 2 + m x - 2 m 2 > 0 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 ⇔ x 2 + m x - 2 m 2 > 0 x 2 - m + 1 x + 2 m - 2 m 2 = 0 ⇔ x = m x = 1 - m
Phương trình đã cho có hai nghiệm x 1 ; x 2 thỏa mãn x 1 2 + x 2 2 > 1
Đáp án C

\(x^2-2\left(2m+1\right)x+4m^2+4m=0\)
Để pt có hai ng pb\(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow4>0\left(lđ\right)\)
\(\Rightarrow\)Pt luôn có hai ng pb với mọi m
\(\left\{{}\begin{matrix}x_1=\dfrac{2\left(2m+1\right)+\sqrt{4}}{2}=2m+2\\x_2=\dfrac{2\left(2m+1\right)-\sqrt{4}}{2}=2m\end{matrix}\right.\)
Có \(\left|x_1-x_2\right|=x_1+x_2\)
\(\Leftrightarrow\left|2m+2-2m\right|=2m+2+2m\)
\(\Leftrightarrow2=4m+2\)
\(\Leftrightarrow m=0\)
Vậy...

\(\Delta'=\left(m-5\right)^2+2m-9=m^2-8m+16=\left(m-4\right)^2\ge0;\forall m\)
Pt đã cho luôn luôn có nghiệm
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-5\right)\\x_1x_2=-2m+9\end{matrix}\right.\)
Do \(x_1\) là nghiệm của pt nên:
\(x_1^2-2\left(m-5\right)x_1-2m+9=0\Rightarrow x_1^2=2\left(m-5\right)x_1+2m-9\)
Thay vào bài toán:
\(2\left(m-5\right)x_1+2m-9+2\left(m-5\right)x_2=4m^2\)
\(\Leftrightarrow2\left(m-5\right)\left(x_1+x_2\right)+2m-9=4m^2\)
\(\Leftrightarrow2\left(m-5\right).2\left(m-5\right)+2m-9=4m^2\)
\(\Leftrightarrow-38m+91=0\)
\(\Rightarrow m=\dfrac{91}{38}\)

Đáp án B
P T ⇔ log 2 2 x 2 - x + 2 m - 4 m 2 + log 2 x 2 + m x - 2 m 2 = 0 ⇔ 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 > 0 ⇔ x 2 - ( m - 1 ) x + 2 m - 2 m 2 = 0 ( x - m ) ( x + 2 m ) > 0 ⇔ [ x = 2 m x = 1 - m x - m x + 2 m > 0
Điều kiện để pt đã cho có 2 nghiệm ⇔ 4 m 2 > 0 x - m x + 2 m > 0 ⇔ m ∈ - 1 ; 1 2 \ 0
Khi đó x 1 2 + x 2 2 > 1 ⇔ 4 m 2 + 1 - m 2 > 1 ⇔ 5 m 2 - 2 m > 0 ⇔ [ m > 2 5 m < 0
Do đó S = - 1 ; 0 ∪ 2 5 ; 1 2 ⇒ A = - 1 + 2 + 1 = 2

Đáp án B
P T ⇔ log 2 2 x 2 - x + 2 m - 4 m 2 + log 2 x 2 + m x - 2 m 2 = 0
⇔ 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 > 0
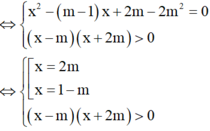
Điều kiện để pt đã cho có 2 nghiệm
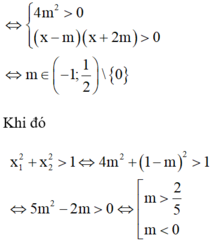
Do đó
S = - 1 ; 0 ∪ 2 5 ; 1 2 ⇒ A = - 1 + 2 + 1 = 2

Δ=(-4m)^2-4(4m^2-m+2)
=16m^2-16m^2+4m-8=4m-8
Để phương trình có hai nghiệm phân biệt thì 4m-8>0
=>m>2
|x1-x2|=2
=>\(\sqrt{\left(x_1-x_2\right)^2}=2\)
=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=2\)
=>\(\sqrt{\left(4m\right)^2-4\left(4m^2-m+2\right)}=2\)
=>\(\sqrt{16m^2-16m^2+4m-8}=2\)
=>\(\sqrt{4m-8}=2\)
=>4m-8=4
=>4m=12
=>m=3(nhận)
Ta có:
\(x^2-2\left(2m+1\right)x+4m^2+4m=0\\ \Leftrightarrow\left(x^2-2mx\right)-2\left(m+1\right)x+4m\left(m+1\right)=0\\ \Leftrightarrow x\left(x-2m\right)-2\left(m+1\right)\left(x-2m\right)=0\\ \Leftrightarrow\left(x-2m\right)\left(x-2m-2\right)=0\Leftrightarrow x_1=2m;...or...x_2=2m\)
\(\Rightarrow\left(x_1-2m\right)\left(x_2-2m\right)=0\Leftrightarrow\left(x_1-2m\right)^2\left(x_2-2m\right)^2=0\Leftrightarrow\left(x_1^2-4mx_1+4m^2\right)\left(x_2^2-4mx_2+4m^2\right)=0\)