Một vật có m=0,5kg được ném lên cao theo phương thẳng đứng từ mặt đất với v = 10 m/s lấy g = 10 m/s². Chọn gốc thế năng tại mặt đất hãy áp dụng định lực bảo toàn cơ năng để. a.Tính cơ năng của vật tại vị trí ném b. Tính độ cao cực đại c. Tính độ cao khi động năng bằng 3 lần thế năng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)Chọn gốc thế năng tại vị trí ném\(\Rightarrow z=0m\).
Cơ năng tại vị trí ném:
\(W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot0,1\cdot4^2+0,1\cdot10\cdot0=0,8J\)
b)Cơ năng ban đầu:
\(W_1=\dfrac{1}{2}mv^2+mgh=\dfrac{1}{2}\cdot0,1\cdot4^2+0,1\cdot10\cdot1=1,8J\)
Cơ năng tại nơi \(W_t=W_đ\):
\(W_2=W_t+W_đ=2W_đ=2\cdot\dfrac{1}{2}mv'^2=mv'^2\)
Bảo toàn cơ năng: \(W_1=W_2\)
\(\Rightarrow1,8=mv'^2\Rightarrow v'=\sqrt{\dfrac{1,8}{0,1}}=3\sqrt{2}\)m/s

1) Vật chỉ chịu tác dụng của trọng lực cơ năng được bảo toàn
Xét tại vị trí ném và vị trí vật lên cao nhất ta có:
\(W_1=W_2\Leftrightarrow\dfrac{1}{2}mv_1^2=mgz_2\Rightarrow z_2=5\left(m\right)\) ( vậy độ cao cực đại mà vật lên được là 5m )
=> Thế năng cực đại: \(mgz_2=0,02.10.5=1\left(J\right)\)
2) a) Tương tự ý 1 bảo toàn cơ năng tại 2 vị trí nêu trên ( bài 1 ):
\(W_1=W_2\Leftrightarrow\dfrac{1}{2}mv_1^2=mgz_2\Rightarrow z_2=\dfrac{16}{5}\left(m\right)\)
b) Bảo toàn cơ năng: \(W_1=W_3\Leftrightarrow\dfrac{1}{2}mv_1^2=\dfrac{4}{3}.\dfrac{1}{2}mv_3^2\Rightarrow v_3=...\) tính nốt
c) Bảo toàn cơ năng: \(W_1=W_4\Leftrightarrow\dfrac{1}{2}mv_1^2=\dfrac{5}{4}mgz_4\Rightarrow z_4=.....\) bạn tính nốt hộ mình

a) Cơ năng tại vị trí cực đại? hay ý bạn là tìm cơ năng ở đâu
Dễ chứng minh được \(h_{max}=h+\dfrac{v_0^2}{2g}=7\left(m\right)\)
b) Vật chỉ chịu tác dụng của trọng lực cơ năng đc bảo toàn: ( chọn mốc thế năng ở điểm ném ) \(W_1=\dfrac{1}{2}mv_1^2+mgz_1=50m\left(J\right)\)
c) Chọn mốc thế năng ở mặt đất:
Bảo toàn cơ năng: \(W_1=W_2\Leftrightarrow\dfrac{1}{2}mv_1^2+mgz_1=\dfrac{3}{2}.\dfrac{1}{2}mgz_2\) => z2=........
d) Chọn mốc thế năng ở mặt đất:
\(W_1=W_2\Leftrightarrow\dfrac{1}{2}mv_1^2+mgz_1=\dfrac{1}{8}mv_1^2+mgz_2\) => z2=.......

\(W=W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}m.10^2=50m\left(J\right)\)
\(W=Wt+Wđ=50m\left(J\right)\)
Mà \(W_t=W_đ\)
\(\Leftrightarrow W_t=W_đ=25m=mgz=10m.z\)
\(\Leftrightarrow z=2,5\left(m\right)\)

a, Bỏ qua sức cản không khí \(\Rightarrow\) Cơ năng bảo toàn
Tại O
\(W_O=\dfrac{mv^2_o}{2}+m.g.h_o=\dfrac{0,2.5^2}{2}+0=2,5\left(J\right)\)
b, Tại \(A\) \(h_A\) max
\(W_O=W_A=m.g.h_A+\dfrac{mv^2_A}{2}\\ \Leftrightarrow2,5=0,2.10.h_A+\dfrac{0,2.0^2}{2}\\ \Leftrightarrow h_A=h_{max}=1,25\left(m\right)\)
c, Tại B
\(Wt_B=2Wđ_B\\ \Rightarrow\left\{{}\begin{matrix}Wt_B-2Wđ_B=0\\Wt_B+Wđ_B=W_B=W_O=2,5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}Wt_B=\dfrac{5}{3}\left(J\right)\Rightarrow m.g.h_b=\dfrac{5}{3}\Rightarrow h_B=\dfrac{5}{6}\left(m\right)\\Wđ_B=\dfrac{5}{6}\left(J\right)\Rightarrow\dfrac{m.v^2_b}{2}=\dfrac{5}{6}\Rightarrow v_B=\dfrac{5\sqrt{3}}{3}\left(m/s\right)\end{matrix}\right.\)

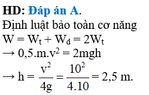
`a// W=W_[đ(max)]=1/2mv_[max] ^2=1/2 .0,5.10^2=25(J)`
`b// W_[đ(max)]=W_[t(max)]`
`<=>25=mgz_[max]`
`<=>25=0,5.10.z_[max]`
`<=>z_[max]=5(m)`
`c// W_[(W_đ=3W_t)]=W_[đ(W_đ=3W_t)]+W_[t(W_đ=3W_t)]=25`
Mà `W_[đ(W_đ=3W_t)]=3W_[t(W_đ=3W_t)]`
`=>4W_[t(W_đ=3W_t)]=25`
`<=>4mgz_[(W_đ=3W_t)]=25`
`<=>4.0,5.z_[(W_đ=3W_t)]=25`
`<=>z_[(W_đ=3W_t)]=12,5(m)`
a/W=Wđ(max)=12mv2max=12.0,5.102=25(J)a/W=Wđ(max)=12mvmax2=12.0,5.102=25(J)
b/Wđ(max)=Wt(max)b/Wđ(max)=Wt(max)
⇔25=mgzmax⇔25=mgzmax
⇔25=0,5.10.zmax⇔25=0,5.10.zmax
⇔zmax=5(m)⇔zmax=5(m)
c/W(Wđ=3Wt)=Wđ(Wđ=3Wt)+Wt(Wđ=3Wt)=25c/W(Wđ=3Wt)=Wđ(Wđ=3Wt)+Wt(Wđ=3Wt)=25
Mà Wđ(Wđ=3Wt)=3Wt(Wđ=3Wt)Wđ(Wđ=3Wt)=3Wt(Wđ=3Wt)
⇒4Wt(Wđ=3Wt)=25⇒4Wt(Wđ=3Wt)=25
⇔4mgz(Wđ=3Wt)=25⇔4mgz(Wđ=3Wt)=25
⇔4.0,5.z(Wđ=3Wt)=25⇔4.0,5.z(Wđ=3Wt)=25
⇔z(Wđ=3Wt)=12,5(m)