giải hệ phương trình:
3y2 + 7xy + 4x - 22 = 4y
x2 + y2 + 3xy = 11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: 2 x y + y 2 − 4 x − 3 y + 2 = 0 x y + 3 y 2 − 2 x − 14 y + 16 = 0 ⇒ 2 x y + y 2 − 4 x − 3 y + 2 = 0 2 x y + 6 y 2 − 4 x − 28 y + 32 = 0
⇒ 5 y 2 − 25 y + 30 = 0 ⇒ y = 3 ; y = 2
Khi y = 3 thì phương trình đầu trở thành 6 x + 9 - 4 x - 9 + 2 = 0 ⇔ x = - 1
Khi y = 2 thì phương trình đầu trở thành 4 x + 4 - 4 x - 6 + 2 = 0
⇔ 0 x = 0 ⇔ x ∈ R
Đáp án cần chọn là: A

+) Xét y = 0 hệ phương trình đã cho trở thành x 2 + 1 = 0 x 2 + 1 x − 2 = 0 (vô lý)
+) Xét y ≠ 0 chia các vế của từng phương trình cho y ta được:
x 2 + 1 y + y + x = 4 x 2 + 1 y y + x − 2 = 1
Đặt x 2 + 1 y = a y + x − 2 = b
⇒ a + b = 2 a b = 1 ⇔ a = 2 − b a ( 2 − a ) = 1 ⇔ b = 2 − a a 2 − 2 a + 1 = 0 ⇔ b = 2 − a a − 1 2 = 0 ⇔ a = b = 1 ⇔ x 2 + 1 y = 1 y + x − 2 = 1 ⇔ y = x 2 + 1 x + y = 3 ⇔ y = x 2 + 1 x + x 2 + 1 = 3 ⇔ y = x 2 + 1 x 2 + x − 2 = 0 ⇔ y = x 2 + 1 x − 1 x + 2 = 0 ⇔ y = x 2 + 1 x = 1 x = − 2 ⇔ x = 1 y = 2 ( t m ) x = − 2 y = 5 ( t m )
Đáp án:D

từ phương trình số 2 ta có
\(\left(x+y\right)\left(x+2y\right)+\left(x+y\right)=0\Leftrightarrow\left(x+y\right)\left(x+2y+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+y=0\\x+2y+1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-y\\x=-2y-1\end{cases}}\)
lần lượt thay vào 1 ta có
\(\orbr{\begin{cases}y^2+7=y^2+4y\\\left(-2y-1\right)^2+7=y^2+4y\end{cases}\Leftrightarrow\orbr{\begin{cases}y=\frac{7}{4}\\3y^2+8=0\end{cases}}}\)
vậy hệ có nghiệm duy nhất \(x=-y=-\frac{7}{4}\)

ĐK: y ≥ 1 3 x + 2 y ≥ 1 ⇔ x ≥ 1 − 2 y y ≥ 1 3
Xét 3 y − 1 + x + 2 y − 1 = 0 ⇔ x = y = 1 3
Thay vào (2) không thỏa mãn
Xét 3 y − 1 + x + 2 y − 1 ≠ 0 ⇔ x ≠ 1 3 y ≠ 1 3
(1) ⇔ y ( x – y ) = y − x 3 y − 1 + x + 2 y − 1
Với x = y, thay vào (2) ta được:
x 4 – 4 x 3 + 7 x 2 − 6 x + 2 = 0 ⇔ ( x – 1 ) 2 ( x 2 – 2 x + 2 ) = 0 ⇔ x = 1
Khi đó: y = 1 (TM). Vậy nghiệm của hệ là (1; 1)
Nên x. y = 1
Đáp án:B

Ta có:\(\left\{{}\begin{matrix}4x^2-xy=2\\y^2-3xy=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(2x-y\right)^2=0\\4x^2-xy=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=y\\4x^2-x.2x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=y\\x^2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}y=1\\y=-1\end{matrix}\right.\\\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\end{matrix}\right.\)

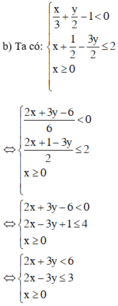
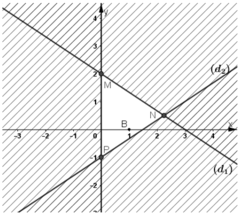
Ta vẽ các đường thẳng 2x + 3y = 6 (d1); 2x – 3y = 3 (d2); x = 0 (trục tung).
Điểm B(1; 0) có tọa độ thỏa mãn tất cả các bất phương trình trong hệ nên ta gạch đi các nửa mặt phẳng bờ (d1); (d2) và trục tung không chứa điểm B.
Miền không bị gạch chéo (tam giác MNP, kể cả cạnh MP và NP, không kể cạnh MN) là miền nghiệm của hệ bất phương trình đã cho.


\(\hept{\begin{cases}x^2-y^2=1-xy\\x^2+y^2=3xy+11\end{cases}}\)