Phân tích đa thức thành nhân tử: \(2x^3-\left(a+2\right)x^2-ax+a^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 1 2023
\(a.\) \(ax^2-a^2x-x+a\)
\(=\left(ax^2-a^2x\right)-\left(x-a\right)\)
\(=ax\left(x-a\right)-\left(x-a\right)\)
\(=\left(ax-1\right)\left(x-a\right)\)
\(b.\) \(18x^3-12x^2+2x\)
\(=2x\left(9x^2-6x+1\right)\)
\(=2x\left(3x-1\right)^2\)
\(c.\) \(x^3-5x^2-4x+20\)
\(=\left(x^3-5x^2\right)-\left(4x-20\right)\)
\(=x^2\left(x-5\right)-4\left(x-5\right)\)
\(=\left(x^2-4\right)\left(x-5\right)\)
\(=\left(x-2\right)\left(x+2\right)\left(x-5\right)\)
\(d.\) \(\left(x+7\right)\left(x+15\right)+15\)
\(=x^2+15x+7x+105+15\)
\(=x^2+22x+120\)
\(=\left(x+10\right)\left(x+12\right)\)
NL
1
T
17 tháng 12 2023
a, \(x^3-2x-y^3+2y\) (sửa đề)
\(=\left(x^3-y^3\right)-\left(2x-2y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-2\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2-2\right)\)
b, \(\left(x-y\right)\left(x+y\right)-4zx+4yz\)
\(=\left(x-y\right)\left(x+y\right)-\left(4zx-4yz\right)\)
\(=\left(x-y\right)\left(x+y\right)-4z\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-4z\right)\)
Bạn xem lại đề câu a giúp mình nha!
XO
16 tháng 10 2020
(x - 5)2 - 4(x - 3)2 + 2(2x - 1)(x - 5) + (2x - 1)2
= [(x - 5)2 + 2(2x - 1)(x - 5) + (2x - 1)2) - [2(x - 3)]2
= (x - 5 + 2x - 1)2 - (2x - 6)2
= (3x - 6)2 - (2x - 6)2
= (3x - 6 - 2x + 6)(3x - 6 + 2x - 6) = x(5x - 12)
16 tháng 10 2020
( x - 5 )2 - 4( x - 3 )2 + 2( 2x - 1 )( x - 5 ) + ( 2x - 1 )2
= [ ( x - 5 )2 + 2( 2x - 1 )( x - 5 ) + ( 2x - 1 )2 ] - 22( x - 3 )2
= ( x - 5 + 2x - 1 )2 - ( 2x - 6 )2
= ( 3x - 6 )2 - ( 2x - 6 )2
= ( 3x - 6 - 2x + 6 )( 3x - 6 + 2x - 6 )
= x( 5x - 12 )
15 tháng 9 2021
\(A=4x^2+6x=2x\left(2x+3\right)\)
\(B=\left(2x+3\right)^2-x\left(2x+3\right)=\left(2x+3\right)\left(2x+3-x\right)=\left(2x+3\right)\left(x+3\right)\)
\(C=\left(9x^2-1\right)-\left(3x-1\right)^2=\left(3x-1\right)\left(3x+1\right)-\left(3x-1\right)^2=\left(3x-1\right)\left(3x+1-3x+1\right)=2\left(3x+1\right)\)
\(D=x^3-16x=x\left(x^2-16\right)=x\left(x-4\right)\left(x+4\right)\)
\(E=4x^2-25y^2=\left(2x-5y\right)\left(2x+5y\right)\)
\(G=\left(2x+3\right)^2-\left(2x-3\right)^2=\left(2x+3-2x+3\right)\left(2x+3+3x-3\right)=6.4x=24x\)
15 tháng 9 2021
\(A=2x\left(2x+3\right)\\ B=\left(2x+3\right)\left(2x+3-x\right)=\left(2x+3\right)\left(x+3\right)\\ C=\left(3x-1\right)\left(3x+1\right)-\left(3x-1\right)^2\\ =\left(3x-1\right)\left(3x+1-3x+1\right)\\ =2\left(3x-1\right)\\ D=x\left(x^2-16\right)=x\left(x-4\right)\left(x+4\right)\\ E=\left(2x-5y\right)\left(2x+5y\right)\\ G=\left(2x+3-2x+3\right)\left(2x+3+2x-3\right)\\ =24x\)
KD
1 tháng 1 2022
a) 2x² - xy + 4x - 2y
<=> (2x² + 4x)-(xy + 2y)
<=> 2x(x + 2) - y(x + 2)
<=> (x + 2)(2x - y)
b) (a²−a+2012)(a²−a+2014)−3
Đặt a²−a+2012 là x , ta có :
x(x + 2) - 3
<=> x² + 2x - 3
<=> x² + 3x - x - 3
<=> x(x + 3) - (x + 3)
<=> (x +3)(x - 1)
Thay x = a²−a+2012 , ta được :
(a²−a+2015)(a²−a+2011)
MT
2
TP
25 tháng 12 2022
\(x^3-8+2x\left(x-2\right)\\ =\left(x-2\right)\left(x^2+2x+4\right)+2x\left(x-2\right)\\ =\left(x-2\right)\left(x^2+2x+4+2x\right)=\left(x-2\right)\left(x^2+4x+4\right)\\ =\left(x-2\right)\left(x+2\right)^2\)
25 tháng 12 2022
=\(\left(x-2\right)\left(x^2+2x+4\right)+2x\left(x-2\right)\)
=\(\left(x-2\right)\left(x^2+4x+4\right)\)
=\(\left(x-2\right)\left(x+2\right)^2\)
TM
1
25 tháng 7 2019
Đặt \(2x^2-x-2=t\)
Ta có:
\(A=\left(t+3\right)\left(t-3\right)+8\)
\(A=t^2-9+8\)
\(A=\left(t-1\right)\left(t+1\right)\)
Thay vào ta được:
\(A=\left(2x^2-x-3\right)\left(2x^2-x-1\right)\)
DA
1
7 tháng 12 2018
Đặt \(x^2-2x+4=a\)
Khi đó \(\left(x^2-2x+3\right)\left(x^2-2x+5\right)-8=\left(a-1\right)\left(a+1\right)-8\)
\(=a^2-1-8\)
\(=a^2-9\)
\(=\left(a-3\right)\left(a+3\right)\)
\(=\left(x^2-2x+4-3\right)\left(x^2-2x+4+3\right)\)
\(=\left(x^2-2x+1\right)\left(x^2-2x+7\right)\)
\(=\left(x-1\right)^2\left(x^2-2x+7\right)\)
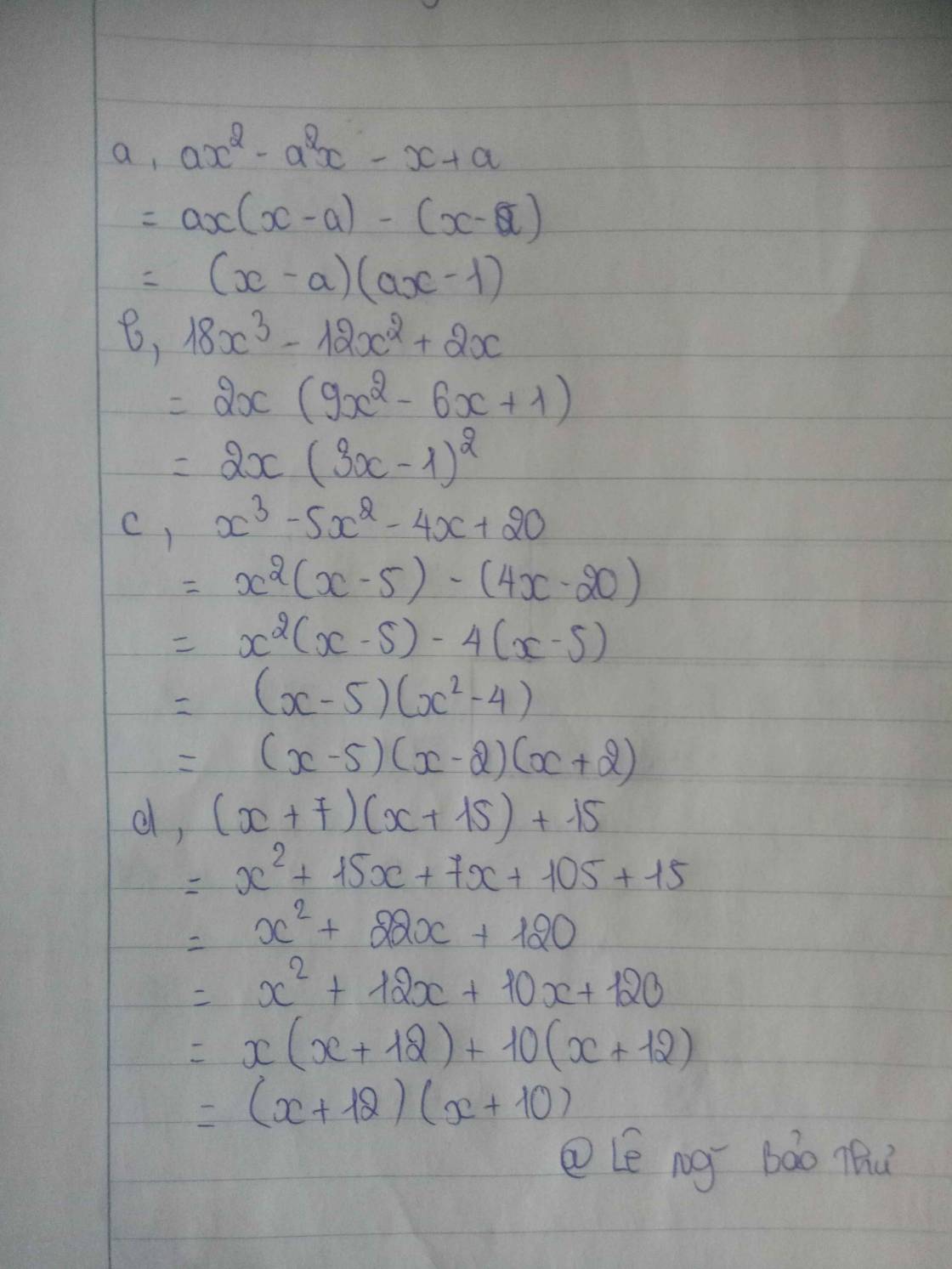
2x3-(a+2)x2-ax+a2
= 2x3-ax2-2x2-ax+a2
=(2x3-ax2)+(-2x2+ax)+(-2ax+a2)
=x2(2x-a)-x(2x-a)-a(2x-a)
=(x2-x-a)(2x-a)