M.n giúp với ạ


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Gió mùa mùa đông:
- Gió mùa mùa đông ở nước ta mà thường được gọi là gió mùa Đông Bắc (thổi đến nước ta theo hướng Đông Bắc, tuy có lúc có nơi hướng gió không hẳn như vậy) là khối không khí với bản chất lạnh, hoạt động chủ yếu vào tháng 11 đến tháng 4 năm sau, làm cho nước ta có 1 mùa đông lạnh giá so với các nước khác cùng vĩ độ.
- Bản chất gió mùa đông bắc là khối không khí cực lục địa (Pc), xuất phát từ cao áp Xi bia thổi về. Đây là 1 vùng rất lạnh và khô, nhiệt độ trung bình mùa đông xuống khoảng -15 đến -400C, độ ẩm riêng 1g/1kg, tạo điều kiện cho việc hình thành 1 cao áp nhiệt lực rất mạnh, áp suất khoảng 1040mb đến 1060mb, chi phối sự phân bố khí áp ở Á châu, làm lu mờ cả hệ thống cao áp cận chí tuyến nơi đây. Điều đáng chú ý là cao áp Xibia nguồn gốc nhiệt lực không dày, không phát triển nên cao, thuờng chỉ đến 1500 – 2000m, đặc điểm này sẽ chi phối phạm vi tác động và đường di chuyển của Pc. Cao áp Xibia xuất hiện từ tháng IX, tăng dần về khí áp và cực đại vào tháng I, lúc tâm thường nằm ở phía Mông Cổ, còn về mùa xuân – thu, khí áp giảm và tâm rút về phía tây bắc, phía tây Xibia. Vì thế, vào mùa xuân – thu xuất hiện thêm các trung tâm áp phụ ở mạn sông Dương Tử (Trường Giang – Trung Quốc).


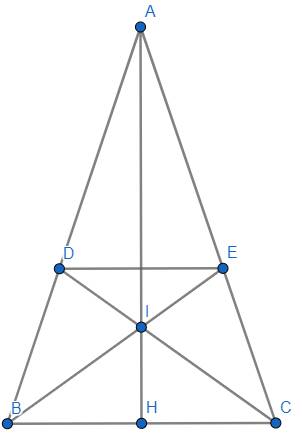
Bài 1. a) Do \(\Delta ABC\) cân tại A (giả thiết) nên \(AB=AC\) và \(\hat{B}=\hat{C}=\dfrac{180^o-\hat{A}}{2}\)
Theo đề bài, \(BD=CE\)
\(\Rightarrow AB-BD=AC-CE\Leftrightarrow AD=AE\).
Suy ra \(\Delta ADE\) cân tại A \(\Rightarrow\hat{D}=\hat{E}=\dfrac{180^o-\hat{A}}{2}\)
Suy ra được : \(\hat{B}=\hat{D}\). Mà hai góc này ở vị trí đồng vị nên \(DE\left|\right|BC\) (điều phải chứng minh).
b) Xét \(\Delta ABE,\Delta ACD\) có : \(\left\{{}\begin{matrix}\hat{A}\text{ chung}\\AD=AE\left(cmt\right)\\AB=AC\left(gt\right)\end{matrix}\right.\Rightarrow\Delta ABE=\Delta ADE\left(c.g.c\right)\)
c) Do \(\Delta ABE=\Delta ACD\left(cmt\right)\) nên \(\hat{DBI}=\hat{ECI}\) (hai góc tương ứng)
Xét các tam giác BID, CIE có : \(\left\{{}\begin{matrix}\hat{DBI}+\hat{DIB}+\hat{BDI}=180^o\\\hat{ECI}+\hat{EIC}+\hat{CIE}=180^o\\\hat{DIB}=\hat{EIC}\left(\text{đối đỉnh}\right);\hat{DBI}=\hat{ECI}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\hat{BDI}=\hat{CIE}\).
Lại xét \(\Delta BID,\Delta CIE\) có : \(\left\{{}\begin{matrix}\hat{BDI}=\hat{CIE}\left(cmt\right)\\BD=CE\left(gt\right)\\\hat{DBI}=\hat{ECI}\left(cmt\right)\end{matrix}\right.\Rightarrow\Delta BID=\Delta CIE\left(g.c.g\right)\) (điều phải chứng minh).
d) Do \(\Delta BID=\Delta CIE\left(cmt\right)\Rightarrow IB=IC\) (hai cạnh tương ứng).
Xét \(\Delta AIB,\Delta AIC\) có : \(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\hat{ABI}=\hat{ACI}\left(cmt\right)\\IB=IC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AIB=\Delta AIC\left(c.g.c\right)\Rightarrow\hat{AIB}=\hat{AIC}\)
⇒ \(AI\) là phân giác của \(\hat{BAC}\) (điều phải chứng minh).
e) Gọi \(H\) là giao điểm của \(AI\) và \(BC\).
Xét \(\Delta AHB,\Delta AHC:\) \(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\hat{IAB}=\hat{IAC}\left(cmt\right)\\AH\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta AHB=\Delta AHC\left(c.g.c\right)\Rightarrow\hat{AHB}=\hat{AHC}\).
Mà : \(\hat{AHB}+\hat{AHC}=180^o\) (hai góc kề bù)
\(\Rightarrow\hat{AHB}=\hat{AHC}=\dfrac{180^o}{2}=90^o\Rightarrow AH\perp BC\Rightarrow AI\perp BC\) (điều phải chứng minh).
f) Để \(BD=DE=CE\) thì \(\Delta BDE\) cân tại \(D\) và \(\Delta CDE\) cân tại \(E\).
Xét với tam giác BDE, khi đó : \(\hat{DBE}=\hat{DEB}\).
Mà : \(\hat{DEB}=\hat{EBC}\) (do \(DE\left|\right|BC\left(cmt\right)\) và hai góc ở vị trí so le trong).
\(\Rightarrow\hat{DBE}=\hat{EBC}\) ⇒ BE là đường phân giác của \(\hat{B}\).
Tương tự với tam giác CDE thì CD sẽ là đường phân giác của \(\hat{C}\).
Vậy : \(BD=DE=CE\) khi và chỉ khi D, E lần lượt là giao điểm của đường phân giác tại các đỉnh B, C với AC, AB.


Giá xe cũ trước khi giảm giá lần 2 là:
684000000:90%=760000000(đồng)
Giá xe cũ trước khi giảm giá lần 1 là:
760000000:95%=800000000(đồng)
Giá xe mới là:
800000000*125%=1000000000(đồng)

\(\frac{1}{12}-\left(-\frac{1}{6}-\frac{1}{4}\right)\)
\(=\frac{1}{12}-\left(-\frac{2}{12}-\frac{3}{12}\right)\)
\(=\frac{1}{12}+\frac{2}{12}+\frac{3}{12}\)
\(=\frac{1}{2}\)
Thanks bạn cute Jeon Koo Koo nhìu nha , tớ cảm ơn pạn rất nhìu :3