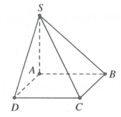
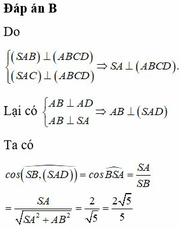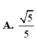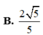cho hình chóp s.abcd có đáy abcd là hình vuông cạnh a, sa vuông góc với mặt phẳng (abcd) và sa = 2a . a,tính cosin của góc tạo bởi hai mặt phẳng (sac) và scd
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 1 2017
Đáp án B
Vì ABCD là hình vuông ⇒ A B ⊥ A D 1
Ta có S A B ⊥ A B C D S A C ⊥ A B C D ⇒ S A ⊥ A B C D ⇒ S A ⊥ A B 2
Từ (1), (2) suy ra A B ⊥ S A D ⇒ S B ; S A D ^ = S B ; S A ^ = B S A ^
Tam giác SAB vuông tại A, có cos B S A ^ = S A S B = S A S A 2 + A B 2 = 2 5 5 .
CM
9 tháng 2 2018
Chọn B.
Phương pháp: Sử dụng định nghĩa góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
CM
15 tháng 7 2018
Đáp án C.
Kẻ C H ⊥ A B .
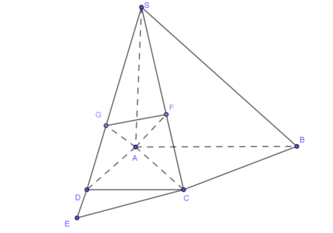
Bằng tính toán hình thang vuông thông thương ta có được:
CM
19 tháng 1 2017
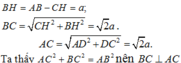
Đáp án C.
Không mất tính tổng quát, giả sử a = 1
Xét hệ trục tọa độ Oxyz với
A 0 ; 0 ; 0 ; D 2 ; 0 ; 0 ;
B 0 ; 1 ; 0 ; S 0 ; 0 ; 5 .
Điểm C thỏa mãn
B C → = 1 2 A D → = 1 ; 0 ; 0
⇒ C 1 ; 1 ; 0 .
mp(SBC) có
n 1 → = S B → ; B C → = 0 ; 1 ; − 5 ; 1 ; 0 ; 0
= 0 ; − 5 ; − 1 .
mp(SCD) có
n 2 → = S D → ; C D → = 2 ; 0 ; − 5 ; 1 ; − 1 ; 0 = 5 ; 5 ; 2 .
Do đó côsin của góc tạo bởi hai mặt phẳng (SBC) và (SCD) bằng:
cos α = n 1 → . n 2 → n 1 . n 2 = 7 2 3 = 21 6 .
CM
21 tháng 7 2019
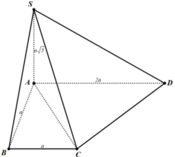
a) Ta có:
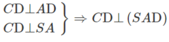
⇒ (SCD) ⊥ (SAD)
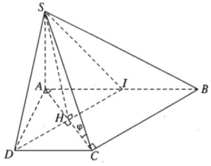
Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).
Vậy (SBC) ⊥ (SAC).
b) Ta có:
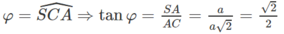
c)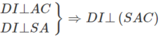 
Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và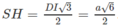 
.
Tam giác SDI có diện tích:
CM
25 tháng 10 2018
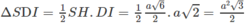
Đáp án A
Do AB // CD => giao tuyến của mặt phẳng (SAB) và (SCD) là đường thẳng qua S và song song với AB.
Dễ thấy Sx ⊥ (DSA) => Góc tạo bởi mặt phẳng (SAB) và (SCD) bằng góc D S A ^ = a r c tan 1 3 = 30 0