Dạng này mình vẫn chưa rõ. Cakpan chỉ giúp mình cái ạ >.<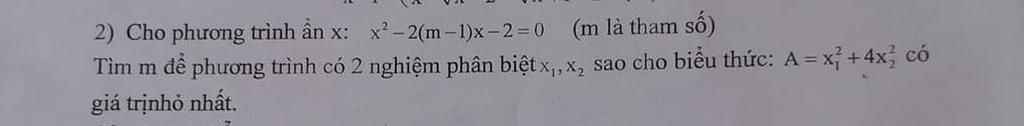
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
S
1
Những câu hỏi liên quan
13 tháng 3 2023
TK:
đây nhé,
1. Sử dụng hai góc kề bù có ba điểm nằm trên hai cạnh là hai tia đối nhau.
2. Ba điểm cùng thuộc một tia hoặc một một đường thẳng
3. Trong ba đoạn thẳng nối hai trong ba điểm có một đoạn thẳng bằng tổng hai đoạn thẳng kia.
4. Hai đoạn thẳng cùng đi qua hai trong ba điểm ấy cùng song song với đường thẳng thứ ba.
5. Hai đường thẳng cùng đi qua hai trong ba điểm ấy cùng vuông góc với đường thẳng thứ ba.
6. Đường thẳng cùng đi qua hai trong ba điểm ấy có chứa điểm thứ ba.
7. Sử dụng tính chất đường phân giác của một góc, tính chất đường trung trực của đoạn thẳng, tính chất ba đường cao trong tam giác
19 tháng 8 2021
Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
19 tháng 8 2021
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.
8 tháng 7 2023
9b:
Kẻ OK vuông góc SA tại K
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=->BD vuông góc SA
mà OK vuông góc SA
nên SA vuông góc (BKD)
=>SA vuông góc BK; SA vuông góc KD
=>((SAB); (SAD))=(BK;KD)
ΔSAC vuông cân tại O nên OK=1/2SA=a/căn 3
ΔBKD cso KO=BO=OD=a/căn 3=1/2*BD
=>ΔBKD vuông tại K
=>góc BKD=90 độ
=>(SAB) vuông góc (SAD)
NH
5
26 tháng 10 2021
đấy là cách tìm số bé, số lớn khi biết tổng và hiệu, phần 2 và phần 3 ở dưới là cách tìm khi tổng, hiệu bị ẩn hoặc ko cùng 1 thời điểm
5 tháng 4 2023
ΔAED vuông tại E nên AE<AD
ΔDFC vuông tại F nên FC<DC
=>AE+FC<AD+DC=AC
3 tháng 7 2016
ko thể vẽ đc vì
trong 2 điểm cho trên một mặt phẳng chỉ có thể ít nhất là 1 đoạn/đường thẳng
28 tháng 9 2020
Xã hội ngày càng phát triển, công nghệ cũng lớn dần theo. Các trang mạng xã hội như Facebook, Báo mới,... trở thành những công cụ tìm kiếm trên Internet ko thể thiếu của mỗi người. Tuy nhiên, các trang mạng xã hội này ko chỉ đáp ứng các nhu cầu thông tin đại chúng mà bên cạnh đó có những thông tin chưa được xác thực hay ko chính xác.
Mặc dù vậy, phần lớn cộng đồng đều tin tưởng nó gần như tuyệt đối. Tiêu biểu nhất như đề bài văn đã nói, có những ng chưa làm rõ sự việc, chưa nghe rõ nhưng đã làm tin đồn lớn dần. Việc này khiến các sự việc ko có thực hay ko chính xác đó trở nên phổ biến rộng rãi và thậm chí có thể gây ra hậu quả khôn lường.
Vì vậy mỗi chúng ta cần cân nhắc lượng thông tin để lưu trữ vào bộ não và quan trọng nhất cần phân biệt thật, giả giữa các nguồn thông tin khổng lồ mà mạng xã hội mang lại cho chúng ta. Đừng nên khẳng định một điều j đó mà mk chưa biết rõ thực hư ra sao nhé.
6 tháng 12 2016
- tỉ lệ nghịch là 2 đại lượng đối nghịch nhau kiểu như cái này tăng thì cái kia giảm (tc thì xét tích tương ứng)
- tỉ lệ thuận là 2 đại lượng cùng tăng và cùng giảm (tc thì xét tỉ số)
Theo cách hiểu của t là thế
LT
7 tháng 12 2016
. Tỉ lệ thuận: Nếu đại lượng x tăng thì đại lượng y cũng tăng, đại lượng x giảm thì đại lượng y cũng giảm. Công thức: y = k.x (k là hằng số khác 0).
. Tỉ lệ nghịch: Nếu đại lượng x tăng lên thì đại lượng y giảm xuống, đại lượng y tăng lên thì đại lượng x giảm. Công thức: y = \(\frac{a}{x}\) hay a = x.y (a là hằng số khác 0)
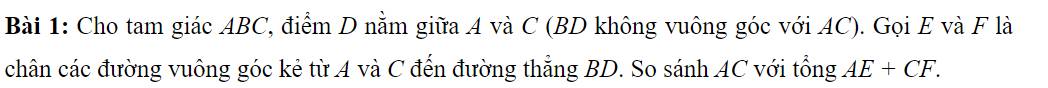
PT có 2 nghiệm phân biệt \(\Leftrightarrow\Delta'=\left(m-1\right)^2+8>0\left(\text{đúng }\forall m\right)\)
Theo Vi-ét: \(\begin{cases} x_1+x_2=2(m-1)=2m-2\\ x_1x_2=-2 \end{cases}\)
Vì \(x_1,x_2\) là nghiệm của PT nên \(\left\{{}\begin{matrix}x_1^2=2\left(m-1\right)x_1+2\\x_2^2=2\left(m-1\right)x_2+2\end{matrix}\right.\)
\(A=x_1^2+4x_2^2=\left(x_1+2x_2\right)^2-4x_1x_2\\ A=\left(x_1+2x_2\right)^2+8\ge8\)
\(\text{Dấu }"="\Leftrightarrow\left\{{}\begin{matrix}x_1=-2x_2\\x_1+x_2=2m-2\\x_1x_2=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=4m-4\\x_2=2-2m\\x_1x_2=-2\end{matrix}\right.\\ \Leftrightarrow\left(4m-4\right)\left(2-2m\right)=-2\\ \Leftrightarrow8\left(m-1\right)^2=2\\ \Leftrightarrow\left(m-1\right)^2=\dfrac{1}{4}\\ \Rightarrow\left[{}\begin{matrix}m=\dfrac{5}{4}\\m=\dfrac{3}{4}\end{matrix}\right.\)
Vậy \(m\in\left\{\dfrac{3}{4};\dfrac{5}{4}\right\}\)