Một hệ gồm một vật nặng khối lượng 100g được gắn với 1 đầu của lo xo đàn hồi có độ cứng 40 N/m, đầu kia của lo xo cố định. Hệ được đặt trên mặt phẳng nhẵn nằm ngang. Ban đầu giữ vật để lò xo dãn 10 cm rồi thả nhẹ. Tính tốc độ của vật khi nó đi qua vị trí mà lò xo không biến dạng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 3 2022
Câu 1.
Cơ năng vật ban đầu:
\(W=W_{đh}=\dfrac{1}{2}k\cdot\left(\Delta x\right)^2=\dfrac{1}{2}\cdot40\cdot0,1^2=0,2J\)
Cơ năng vật tại nơi đi qua vị trí lò xo không biến dạng:
\(W'=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot0,1\cdot v^2=0,05v^2\left(J\right)\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow0,2=0,05v^2\Rightarrow v=2\)m/s
Câu 2.
Vật được ném lên từ mặt đất\(\Rightarrow z=0m\)
Cơ năng vật ban đầu:
\(W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot0,5\cdot2^2=1J\)
19 tháng 3 2022
Động năng:
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot0,1\cdot0^2=0J\)
Thế năng đàn hồi:
\(W_{đh}=\dfrac{1}{2}k\left(\Delta x\right)^2=\dfrac{1}{2}\cdot200\cdot0,05^2=0,25J\)
Cơ năng hệ:
\(W=W_đ+W_{đh}=0+0,25=0,25J\)
DM
26 tháng 2 2021
Cơ năng \(W=\dfrac{1}{2}kx^2+\dfrac{1}{2}mv^2\)
Vật nằm ngang v = 0 => \(W=\dfrac{1}{2}kx^2=\dfrac{1}{2}\cdot200\cdot0,05^2=0,25\left(J\right)\)
TP
26 tháng 2 2021
Đáp án : A) 25.10^-2
B. 50.10^-2
C. 100.10^-2
D. 200.10^-2
Vậy đáp án A ạ?
cm C. 
cm
VT
3 tháng 9 2018
Đáp án C
Phương pháp: Sử dụng phương pháp động lực học và phương pháp bảo toàn năng lượng.
Cách giải:
Hai vật chuyển động đến vị trí vận tốc cực đại, vị trí đó là :
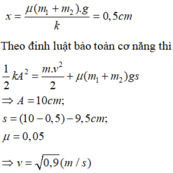
Khi hai vật tách nhau ra, vật 1 tiếp tục dao động, vật 2 chuyển động chậm dần rồi dừng lại.
Gia tốc chuyển động của vật 2 là:
Thời gian để vật 2 chuyển động đến khi dừng lại là:
VT
23 tháng 3 2019
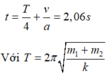
Phương pháp: Sử dụng phương pháp động lực học và phương pháp bảo toàn năng lượng.
Cách giải:
Hai vật chuyển động đến vị trí vận tốc cực đại, vị trí đó là
Khi hai vật tách nhau ra, vật 1 tiếp tục dao động, vật 2 chuyển động chậm dần rồi dừng lại.
Gia tốc chuyển động của vật 2 là:
Đáp án C
`m=100g=0,1kg`
`k=40N//m`
`l=10cm=0,1m`
`v=?(m//s)`
___________________________________
`@` Cơ năng của vật:
\(W=\dfrac{1}{2}k\Delta l^2=\dfrac{1}{2}.40.0,1^2=0,2\left(J\right)\)
`@` Vận tốc của vật khi nó đi qua vị trí mà lò xo không biến dạng:
\(W=\dfrac{1}{2}mv^2\)
\(v=\sqrt{\dfrac{2W}{m}}=\sqrt{\dfrac{2.0,2}{0,1}}=2\left(\dfrac{m}{s}\right)\)