Giải phương trình: tanx + tan2x - tan3x = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bước 1: Sử dụng công thức tan(A + B) để biểu diễn các hàm tan của tổng hai góc. Ta có: tan(A + B) = (tanA + tanB) / (1 - tanA * tanB)
Bước 2: Áp dụng công thức trên vào phương trình ban đầu, ta có: tan(2x + 3x) * tan(7x) = (tan2x + tan3x) / (1 - tan2x * tan3x) + tan7x
Bước 3: Đơn giản hóa phương trình: tan(5x) * tan(7x) = (tan2x + tan3x) / (1 - tan2x * tan3x) + tan7x
Bước 4: Sử dụng công thức tan(A + B) và tan(A - B) để biểu diễn các hàm tan của tổng và hiệu hai góc. Ta có: tan(A + B) = (tanA + tanB) / (1 - tanA * tanB) tan(A - B) = (tanA - tanB) / (1 + tanA * tanB)
Bước 5: Áp dụng công thức trên vào phương trình, ta có: (tan5x + tan7x) / (1 - tan5x * tan7x) = (tan2x + tan3x) / (1 - tan2x * tan3x) + tan7x
Bước 6: Đơn giản hóa phương trình và đưa về dạng tổng cộng các hàm tan: (tan5x + tan7x) * (1 - tan2x * tan3x) = (tan2x + tan3x) * (1 - tan5x * tan7x) + tan7x * (1 - tan2x * tan3x) * (1 - tan5x * tan7x)
Bước 7: Đơn giản hóa và rút gọn phương trình. Ta có: tan5x - tan2x * tan3x * tan5x + tan7x - tan2x * tan3x * tan7x = tan2x + tan3x - tan2x * tan3x + tan7x - tan2x * tan3x * tan7x + tan7x - tan2x * tan3x * tan7x
Bước 8: Rút gọn và sắp xếp các thành phần. Ta có: tan5x - tan2x * tan3x * tan5x - tan2x - tan3x + tan2x * tan3x + tan7x - tan2x * tan3x * tan7x - tan7x = 0
Bước 9: Đơn giản hóa và rút gọn phương trình. Ta có: tan5x - tan2x - tan3x + tan7x - tan2x * tan3x * (tan5x + tan7x) = 0
Bước 10: Phân tích phương trình và tìm các giá trị của x thỏa mãn.

Lời giải:
$\tan 3x-\tan x=2$
$\Leftrightarrow \frac{3\tan x-\tan ^3x}{1-3\tan ^2x}-\tan x=2$
Đặt $\tan x=a$ thì:
$\frac{3a-a^3}{1-3a^2}-a=2$
$\Leftrightarrow a^3+3a^2+a-1=0$
$\Leftrihgtarrow a^2(a+1)+2a(a+1)-(a+1)=0$
$\Leftrightarrow (a+1)(a^2+2a-1)=0$
$\Leftrightarrow a=-1$ hoặc $a=-1\pm \sqrt{2}$
Đến đây thì đơn giản rồi.
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}+k\pi\\x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{3}\end{matrix}\right.\)
\(\dfrac{sin3x}{cos3x}-\dfrac{sinx}{cosx}=2\)
\(\Rightarrow sin3x.cosx-cos3x.sinx=2cos3x.cosx\)
\(\Leftrightarrow sin2x=cos4x-cos2x\)
\(\Leftrightarrow cos^22x-sin^22x-sin2x-cos2x=0\)
\(\Leftrightarrow\left(sin2x+cos2x\right)\left(cos2x-sin2x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)=0\\cos\left(2x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)

a, cos2x - sin7x = 0
⇔ cos2x = sin7x
⇔ cos2x = cos \(\left(7x-\dfrac{\pi}{2}\right)\)
⇔ \(\left[{}\begin{matrix}7x-\dfrac{\pi}{2}=2x+k2\pi\\7x-\dfrac{\pi}{2}=-2x+k2\pi\end{matrix}\right.\) với k là số nguyên
⇔ \(\left[{}\begin{matrix}x=\dfrac{\pi}{10}+\dfrac{k.2\pi}{5}\\x=\dfrac{\pi}{18}+\dfrac{k2\pi}{9}\end{matrix}\right.\) với k là số nguyên

Đáp án A
Tìm điều kiện để phương trình ban đầu có nghĩa. Giải trực tiếp phương trình đã cho và đối chiếu điều kiện để suy ra nghiệm cần tìm.
Điều kiện
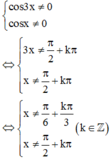
Ta có

Đối chiếu với điều kiện
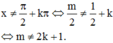
Khi đó
![]()
Từ
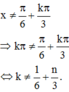
Do vế phải của biểu thức trên không là số nguyên nó luôn đúng.
Vậy nghiệm của phương trình
![]()
Giải theo công thức tan(x+2x)=(tanx+tan2x)/(1-tanx.tan2x) có vẻ nhanh hơn đó.
Nhưng nhớ phải đặt điều kiện cho 3 cái cos dưới mẫu khác 0 (đk riêng của pt lượng giác)
Giải phương trình : sin5x-sin3x=0