Cho tam giác PQR cân tại P. Trên cạnh PQ vẽ T sao cho QT = 2PT. Vẽ QG vuông góc với RT. Gọi M là trung điểm của PG. Tính góc PMQ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 12 2023
Sửa đề: MK\(\perp\)PQ; MN\(\perp\)PR
a: ta có: ΔPQR vuông tại P
=>\(QR^2=PQ^2+PR^2\)
=>\(QR^2=8^2+6^2=100\)
=>\(QR=\sqrt{100}=10\left(cm\right)\)
Ta có: ΔRPQ vuông tại P
mà PM là đường trung tuyến
nên \(PM=\dfrac{RQ}{2}=5\left(cm\right)\)
b: Xét tứ giác PNMK có
\(\widehat{PNM}=\widehat{PKM}=\widehat{NPK}=90^0\)
=>PNMK là hình chữ nhật
c: Xét ΔRPQ có
M là trung điểm của RQ
MK//RP
Do đó: K là trung điểm của PQ
=>PK=KQ(1)
Ta có: PKMN là hình chữ nhật
=>PK=MN(2)
Từ (1) và (2) suy ra KQ=MN
Ta có: PK//MN
K\(\in\)PQ
Do đó: NM//KQ
Xét tứ giác KQMN có
KQ//MN
KQ=MN
Do đó: KQMN là hình bình hành
=>QN cắt MK tại trung điểm của mỗi đường
mà O là trung điểm của MK
nên O là trung điểm của QN
=>OQ=ON
Xét tứ giác PMQH có
K là trung điểm chung của PQ và MN
=>PMQH là hình bình hành
Hình bình hành PMQH có PQ\(\perp\)MH
nên PMQH là hình thoi
5 tháng 12 2023
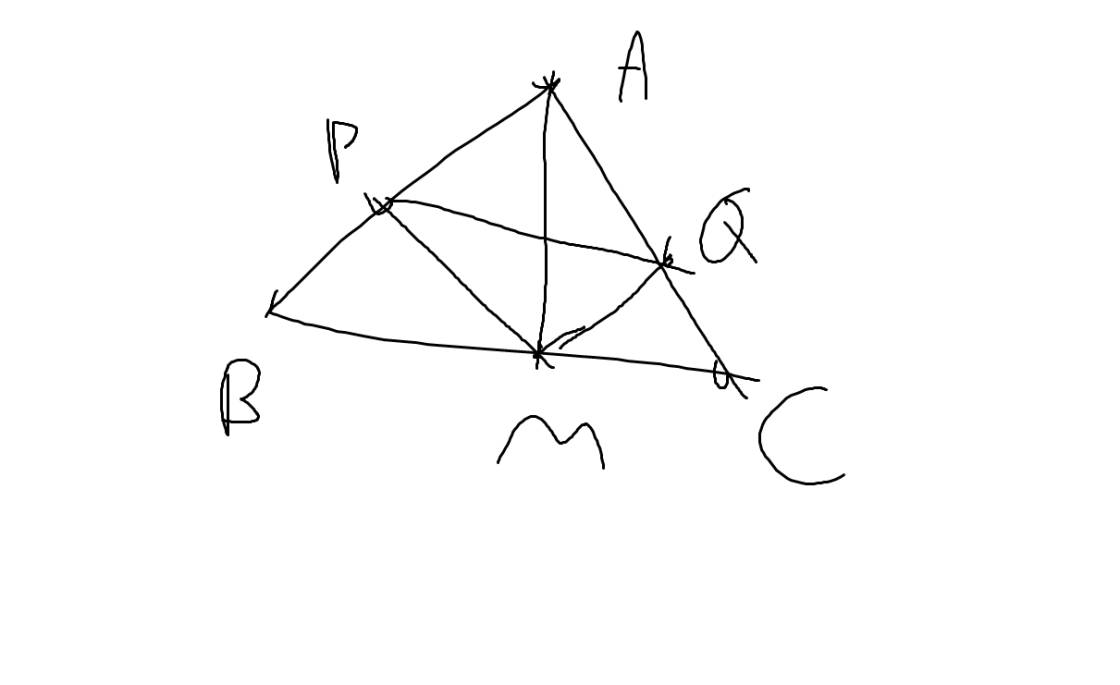
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔPAM vuông tại P và ΔQAM vuông tại Q có
AM chung
\(\widehat{PAM}=\widehat{QAM}\)
Do đó: ΔPAM=ΔQAM
=>PA=QA và MP=MQ
b: AP=AQ
=>A nằm trên đường trung trực của PQ(1)
MP=MQ
=>M nằm trên đường trung trực của PQ(2)
Từ (1) và (2) suy ra AM là đường trung trực của PQ
=>AM\(\perp\)PQ
30 tháng 10 2023
Ta có; ΔABC vuông cân tại C
mà CD là đường trung tuyến
nên CD\(\perp\)AB và CD là phân giác của \(\widehat{ACB}\)
=>\(\widehat{ACD}=\widehat{BCD}=\dfrac{90^0}{2}=45^0\)
Gọi O là giao điểm của CM với FE
Xét tứ giác CEMF có
\(\widehat{CEM}=\widehat{CFM}=\widehat{FCE}=90^0\)
=>CEMF là hình chữ nhật
=>CM cắt EF tại trung điểm của mỗi đường và CM=EF
=>O là trung điểm chung của CM và EF và CM=EF
=>OM=OC=OE=OF
=>O là tâm đường tròn ngoại tiếp tứ giác CFME
\(\widehat{CEM}=\widehat{CFM}=\widehat{CDM}=90^0\)
Do đó: C,E,M,F,D cùng thuộc đường tròn đường kính CM
=>C,E,M,F,D cùng thuộc (O)
=>D thuộc (O)
Xét (O) có
ΔDFE nội tiếp
FE là đường kính
Do đó: ΔDFE vuông tại D
Xét tứ giác FDEC có
\(\widehat{FCE}+\widehat{FDE}=180^0\)
=>FDEC là tứ giác nội tiếp
=>\(\widehat{DFE}=\widehat{DCE}=\widehat{DCA}=45^0\)
Xét ΔDFE vuông tại D có \(\widehat{DFE}=45^0\)
nên ΔDFE vuông cân tại D