Cho 5 đường thẳng đôi một cắt nhau gọi số giao điểm là m
Tính giá trị nhỏ nhất của m. Tính giá trị lớn nhất của m
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 6 2017
+ Lớn nhất :
Vì M là điểm nên điểm M là giao điểm của các đoạn thẳng nên n = 1
Vậy .....
+Nhỏ nhất
Để n nhỏ nhất thì n = 0 khi và chỉ khi số đường thằng đã cho không đi qua M ( vì đề bài đâu yêu cầu n thuộc N* )
Suy ra n = 0
Vậy ...........
CM
6 tháng 12 2019
Đáp án B
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số y = f(x) trên [a;b]
+) Bước 1: Tính y’, giải phương trình y' = 0 ⇒ xi ∈ [a;b]
+) Bước 2: Tính các giá trị f(a); f(b); f(xi)
+) Bước 3:
CM
24 tháng 12 2017
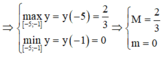
Chọn C
.
Vì 
nên phương trình 
có 2 nghiệm phân biệt.
Do đó hàm số có hai điểm cực trị 
.
Giả sử hàm số có hai điểm cực trị lần lượt là 
và 
, với 
, 
là nghiệm của phương trình 
.
Thực hiện phép chia 
cho 
ta được : 
.
Khi đó ta có: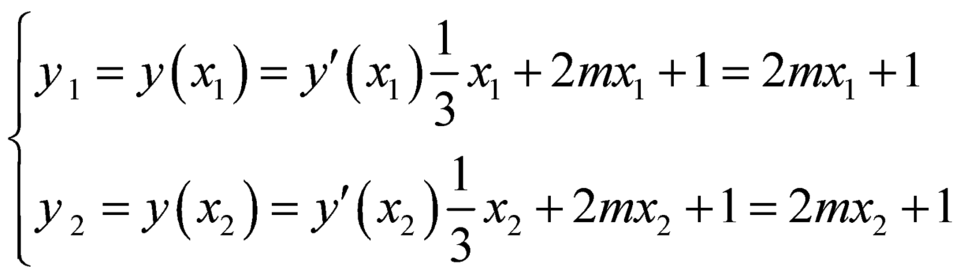 
.
Ta thấy, toạ độ hai điểm 
và 
thoả mãn phương trình 
.
Do đó, phương trình đường thẳng qua hai điểm cực trị là 
.
Ta thấy 
luôn qua 
.
Đặt 
.
.
Xét hàm số 
, 
.
, 
.
Suy ra hàm số 
liên tục và đồng biến trên 
.
Do đó 
.
Vậy 
đạt giá trị lớn nhất 
.
Số giao điểm là:
\(\frac{5.\left(5-1\right)}{2}=10\)(điểm)