Một người đi xe máy từ tỉnh A đến tỉnh B với vận tốc dự định là 40km/h. Sau khi đi được 1 giờ với vận tốc ấy, người đó nghỉ 15 phút và tiếp tục đi. Để đến B kịp thời gian đã định, người đó phải tăng vận tốc thêm 5 km/h. Tính quãng đường từ tỉnh A đến tỉnh B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi độ dài quãng đường AB là x (x>0) (km)
Vậy thời gian dự định người đó đi AB là x/50 (h)
Vậy quãng đường người đó đã đi là 2 x 50 = 100 (km)
Vậy quãng đường còn lại người đó phải đi là: x-100 (km)
Thời gian còn lại của người đó trên thực tế là: (x-100)/60 + 1/3 (h)
Ta có phương trình:
\(\frac{x-100}{60}+\frac{1}{3}=\frac{x-100}{50}\)
\(x=200\left(tmdk\right)\)
Vậy độ dài quãng đường AB là 200 km

Gọi độ dài quãng đường là x
Thời gian dự định là x/35
Theo đề, ta có phương trình:
\(\dfrac{x}{35}=\dfrac{4}{3}+\dfrac{x-\dfrac{4}{3}\cdot35}{42}\)
=>1/35x=4/3+1/42x-10/9
=>1/210x=2/9
=>x=140/3

Đáp án A
Gọi vận tốc ban đầu của người đó là x (km/h) (x > 0).
Thời giạn dự định người đó đi hết quãng đường là 90/x (h).
Quãng đường người đó đi được sau 1 giờ là x (km).
Quãng đường còn lại người đó phải tăng tốc là 90 – x (km).
Vận tốc của người đó sau khi tăng tốc là x + 4 (km/h).
Thời gian người đó đi hết quãng đường còn lại là 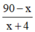 (h).
(h).
Theo đề bài ta có phương trình:
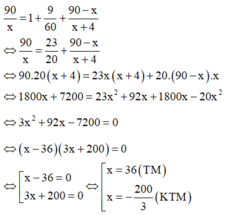
Vậy vận tốc lúc đầu của người đó là 36 km/h.

Gọi quãng đường đi từ tỉnh A đến tỉnh B là: a (km, a>0)
Thời gian đi từ tỉnh A đến tỉnh B theo dự định là: \(\dfrac{a}{40}\) (h)
Thời gian đi từ tỉnh A đến B sau 1h là: \(\dfrac{a-40}{45}\) (h)
Theo bài ra, ta có phương trình:
\(\dfrac{a}{40}=1+\dfrac{1}{4}+\dfrac{a-40}{45}\)
<=>\(\dfrac{9a}{360}=\dfrac{360}{360}+\dfrac{90}{360}+\dfrac{8\left(a-40\right)}{360}\)
<=> \(9a=360+90+8a-320\)
<=> \(a=130\)
Vậy quãng đường đi từ tỉnh A đến tỉnh B dài 130 km.

10p = 1/6h
Thời gian đi dự định: \(\dfrac{AB}{48}h\)
Thời gian đi thực tế: \(1+\dfrac{1}{6}+\dfrac{AB-48}{48+6}\)\(=\dfrac{7}{6}+\dfrac{AB-48}{54}h\)
Ta có: \(\dfrac{AB}{48}=\dfrac{7}{6}+\dfrac{AB-48}{54}\Leftrightarrow\dfrac{AB}{432}=\dfrac{5}{18}\)
\(\Rightarrow AB=120km\)
Gọi quãng đường AB là a(km)(a>0)
Theo đề bài ta có:
\(\dfrac{a}{48}=\dfrac{1}{6}+1+\dfrac{a-48.1}{48+6}\)
\(\Rightarrow\dfrac{a}{48}=\dfrac{a+15}{54}\)
\(\Rightarrow48a+720=54a\Rightarrow a=120\left(nhận\right)\)
Vậy...
Gọi x km là quãng đường AB (x>0)
Thời gian dự định đi: x/40 (h)
Quãng đường còn phải đi sau khi đã đi 1 giờ: x - 40 (km)
Vận tốc mới: 40 + 5 = 45 (km/h)
Thời gian đi đến B với vận tốc mới: (x - 40) / 45 (h)
15 phút = 1/4 h
Từ các kết quả trên ta có phương trình biểu diễn:
1 + (1/4) + {(x - 40) / 45} = (x/40)
( một giờ đi với vận tốc 40 km + 15 phút nghỉ + thời gian đi với vận tốc mới thì bằng thời gian dự định)
Sau khi quy đồng, khử mẫu và rút gọn ta sẽ có:
5x = 650
=> x = 130 (thỏa mãn)
=> Quãng đường AB dài 130 km.
QĐ dài 130 nha