(2,5 điểm) 1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Một tổ sản xuất phải làm xong $4$ $800$ bộ đồ bảo hộ y tế trong một số ngày quy định. Thực tế, mỗi ngày tổ đó đã làm được nhiều hơn $100$ bộ đồ bảo hộ y tế so với số bộ đồ bảo hộ y tế phải làm trong một ngày theo kế hoạch. Vì thế $8$ ngày trước khi hết thời hạn, tổ sản xuất đã làm xong $4$ $800$ bộ đồ bảo hộ y tế đó. Hỏi theo kế hoạch, mỗi ngày tổ sản xuất phải làm bao nhiêu bộ đồ bảo hộ y tế? (Giả định rằng số bộ đồ bảo hộ y tế mả tổ đó làm xong trong mỗi ngày là bằng nhau.)
2) Một thùng nước có dạng hình trụ với chiều cao $1,6$ m và bán kính đáy $0,5$ m. Người ta sơn toàn bộ phía ngoài mặt xung quanh của thùng nước này (trừ hai mặt đáy). Tính diện tích bề mặt được sơn của thùng nước (lấy $\pi \approx 3,14$).


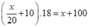
1, Gọi số bộ đồ tổ sản xuất phải làm mỗi ngày theo kế hoạch là x ( x ϵ N* )
Gọi số bộ đồ tổ sản xuất làm được mỗi ngày theo thực tế là x + 100 ( bộ )
Thời gian tổ sản xuất làm theo kế hoạch là \(\dfrac{4800}{x}\)( ngày ) (1)
Thời gian tổ sản xuất làm thực tế là \(\dfrac{4800}{x+100}\)( ngày ) (2)
Thực tế, tổ sản xuất đã hoàn thành trước 8 ngày nên từ (1) và (2), ta có phương trình:
\(\dfrac{4800}{x}-\dfrac{4800}{x+100}=8\)
Sau đó giải như bth là xong ^^
2) Diện tích bề mặt hình trụ là:
2πrh = 2.3,14.0,5.1,6 ≈ 5,024 ( m2 )
Vậy diện tích bề mặt được sơn của thùng nước là 5,024 m2