Các achị giúp e phân c) vs d) ạ. Cảm ơn nhiều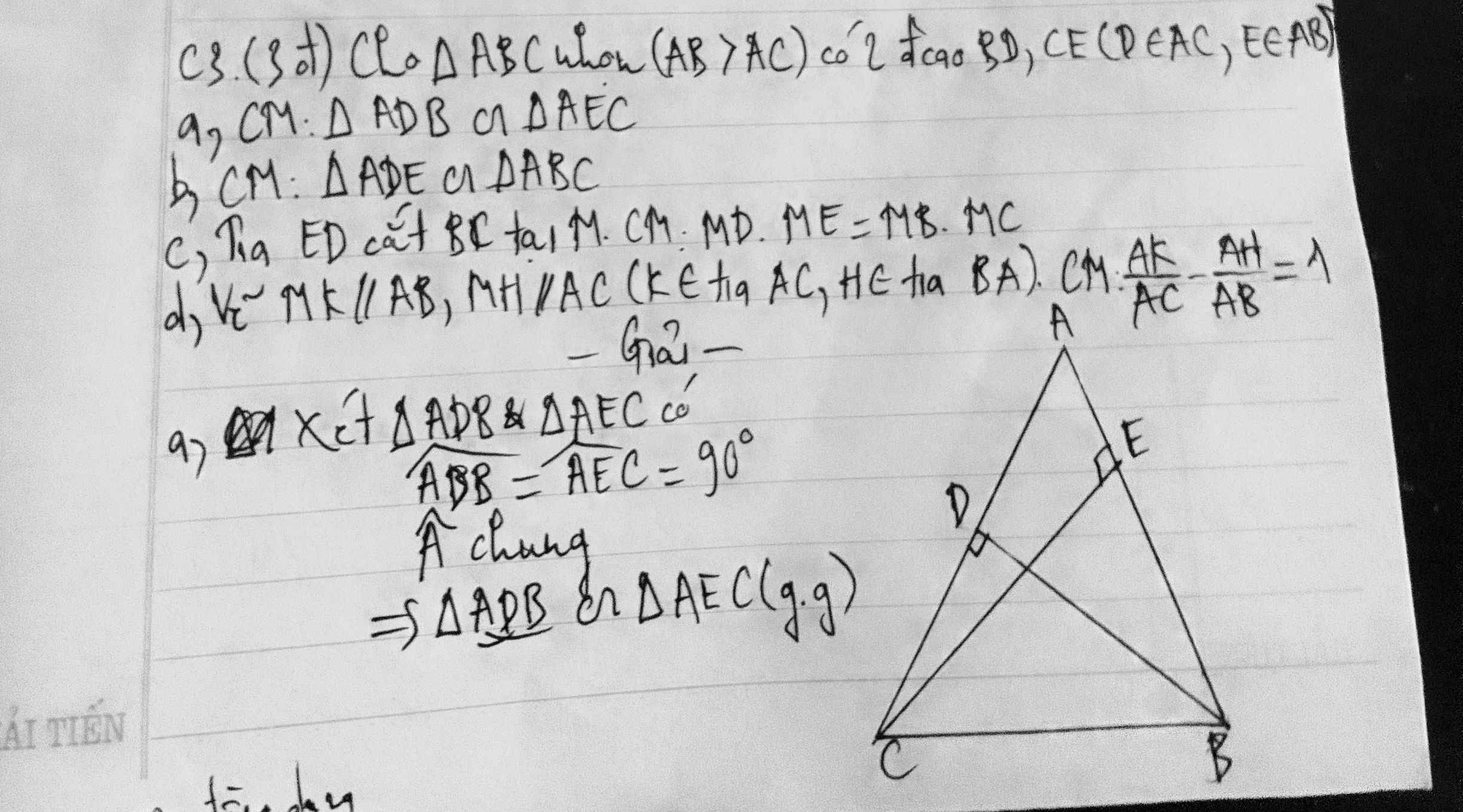 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
1
NT
0
25 tháng 5 2021
`A=1/(x+sqrtx)+(2sqrtx)/(x-1)-1/(x-sqrtx)`
`=(sqrtx-1+2x-sqrtx-1)/(sqrtx(x-1))`
`=(2x-2)/(sqrtx(x-1))`
`=2/sqrtx`
`b)A=1`
`<=>2/sqrtx=1`
`<=>sqrtx=2`
`<=>x=4(tm)`
H9
HT.Phong (9A5)
CTVHS
7 tháng 12 2023
Bài 3:
a) \(159-\left(25-x\right)=43\)
\(\Rightarrow25-x=159-43\)
\(\Rightarrow25-x=116\)
\(\Rightarrow x=25-116\)
\(\Rightarrow x=-91\)
b) \(\left(79-x\right)-43=-\left(17-52\right)\)
\(\Rightarrow\left(79-x\right)-43=-\left(-35\right)\)
\(\Rightarrow79-x=35+43\)
\(\Rightarrow79-x=78\)
\(\Rightarrow x=79-78\)
\(\Rightarrow x=1\)
c) \(-\left(-x+13-142\right)+18=55\)
\(\Rightarrow-\left(-x+13-142\right)=55-18\)
\(\Rightarrow x-13+142=37\)
\(\Rightarrow x+129=37\)
\(\Rightarrow x=37-129\)
\(\Rightarrow x=-92\)
NM
1
23 tháng 1 2022
Bài 1:
a, Xét ΔABC và ΔCDA có:
AB=CD(gt)
AD=BC(gt)
Chung AC
⇒ΔABC = ΔCDA (c.c.c)
b, ΔABC = ΔCDA(cma) ⇒\(\widehat{ACB}=\widehat{CAD}\) ( 2 góc tương ứng)
Mà 2 góc này ở vị trị so le trong với nhau ⇒ AD // BC
23 tháng 1 2022
Bn vẽ hình bài 1 cho mik đc ko ạ! Mik chưa hiểu rõ lắm!
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2023
\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^9}\)
\(\Rightarrow2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^8}\)
\(\Rightarrow2A-A=1-\dfrac{1}{2^9}\)
\(\Rightarrow A=1-\dfrac{1}{2^9}=\dfrac{511}{512}\)
\(\Rightarrow\left(a+b\right)_{min}=511+512=1023\)
14 tháng 11 2021
Xét △ABC có : E là trung điểm AC (gt)
F là trung điểm BC (gt)
=> EF là đường trung bình của △ABC
=> EF // AB mà D ∈ AB
=> EF // AD
Xét △ABC có : D là trung điểm AB (gt)
F là trung điểm BC (gt)
=> DF là đường trung bình của △ABC
=> DF // AC mà E ∈ AC
=> DF // AE
Xét tứ giác ADFE có : EF // AD (cmt)
DF // AE (cmt)
=> Tứ giác ADFE là hình bình hành (DHNB)
10 tháng 1 2022
Xét △ABC có : E là trung điểm AC (gt)
F là trung điểm BC (gt)
=> EF là đường trung bình của △ABC
=> EF // AB mà D ∈ AB
=> EF // AD
Xét △ABC có : D là trung điểm AB (gt)
F là trung điểm BC (gt)
=> DF là đường trung bình của △ABC
=> DF // AC mà E ∈ AC
=> DF // AE
Xét tứ giác ADFE có : EF // AD (cmt)
DF // AE (cmt)
=> Tứ giác ADFE là hình bình hành (DHNB)
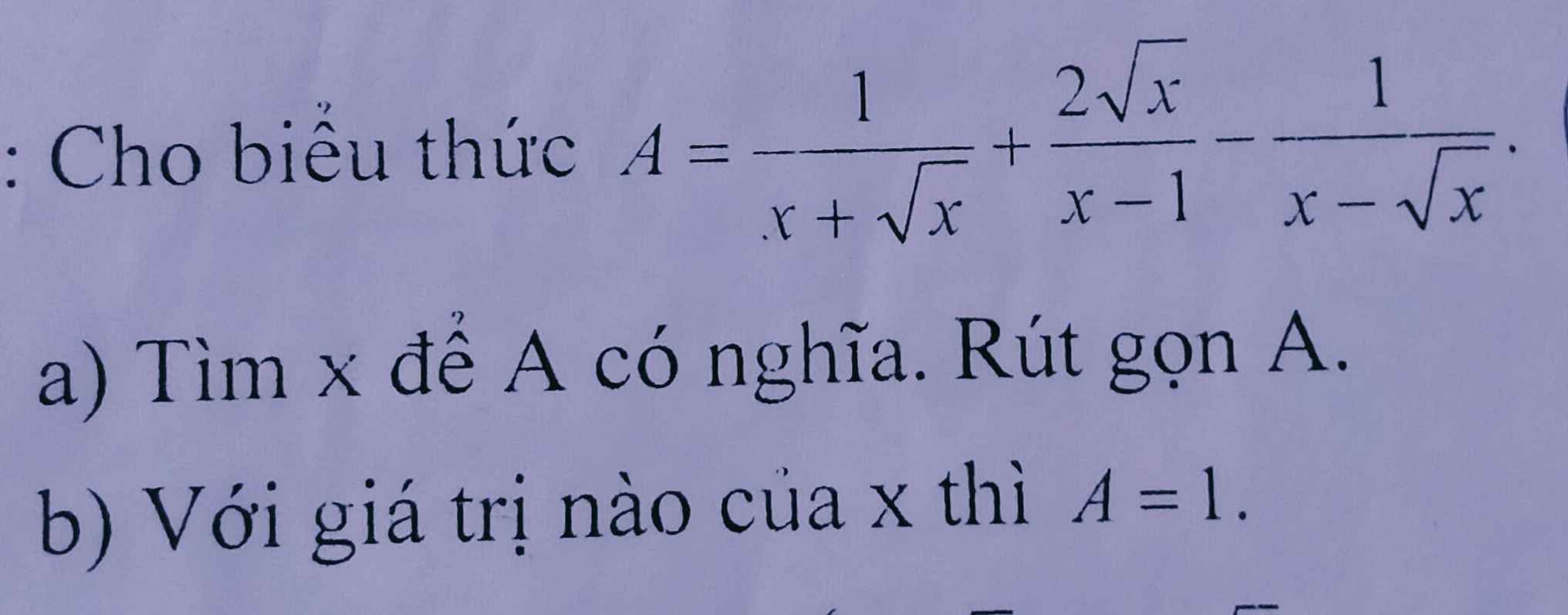
b: góc BDC=góc BEC=90độ
=>BEDC nội tiếp
=>góc ADE=góc ABC
=>ΔADE đồng dạng với ΔABC
b: Xét ΔMDC và ΔMBE có
góc MDC=góc MBE
góc M chung
=>ΔMDC đồng dạng với ΔMBE
=>MD/MB=MC/ME
=>MD*ME=MB*MC