Gọi hình chóp S.MNPQ. Sm vuông góc với (MNPQ) . \(SA=2a\sqrt{3}\). MNPQ là hcn. MN=2a. MP=4a. Gọi MH.NK lần lượt là đường cao của tam giác SMN và SMQ. Tính Diện tích tam giác MHK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
16 tháng 9 2018
Phương pháp:
Tính thể tích V S . A B C
Tính thể tích V S . A M N theo công thức tỉ lệ thể tích
Tính thể tích V A . B C M N và suy ra kết luận
Cách giải:
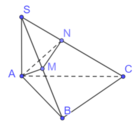
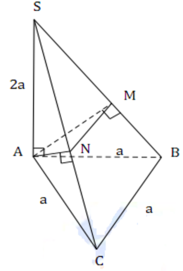
Xét tam giác SAB và SAC là các tam giác vuông tại A có hai cạnh góc vuông là a và 2a nên
![]()
Tam giác SAB vuông tại có đường cao AM
Khi đó ![]()
Tương tự ![]()
Lại có ![]()
Mặt khác 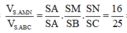
![]()
Do đó ![]()
![]()
Chọn C.

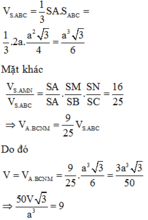
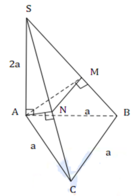
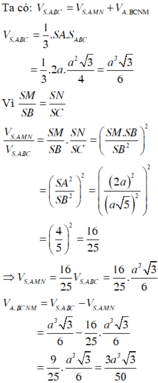
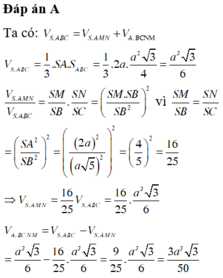
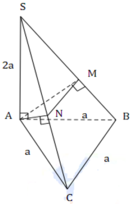
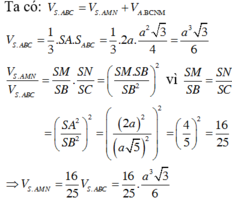
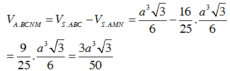
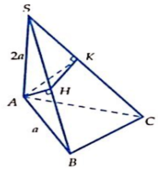


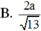


Mik nghĩ là : \(SM\perp\) đáy và MK là đường cao của \(\Delta SMQ\)
\(MQ=\sqrt{MP^2-MN^2}=\sqrt{16a^2-4a^2}=2\sqrt{3}a=SM\)
\(\Delta SMN\perp\) tại M ; \(MH\perp SN\) có :
\(MH=\dfrac{SM.MN}{\sqrt{SM^2+MN^2}}=\dfrac{2a\sqrt{3}.2a}{\sqrt{12a^2+4a^2}}=\sqrt{3}a\)
Làm tương tự ; tính được : \(MK=\sqrt{6}a\) . Cần tính HK
Tính được : \(SH=3a;MK=SK=\sqrt{6}a\) .
Tính được : \(SN=NQ=4a;SQ=2\sqrt{6}a\) \(\Rightarrow cos\widehat{S}=\dfrac{\sqrt{6}}{4}\) . Khi đó :
\(HK^2=SK^2+SH^2-2SK.SH.cos\widehat{S}=15a^2-6\sqrt{6}a^2.\dfrac{\sqrt{6}}{4}=6a^2\Rightarrow HK=\sqrt{6}a\)
\(\Delta MHK\) có : p = \(\dfrac{MH+HK+MK}{2}=\dfrac{2\sqrt{6}+\sqrt{3}}{2}a\)
Suy ra : \(S=\sqrt{p\left(p-MH\right)\left(p-MK\right)\left(p-HK\right)}=\dfrac{3\sqrt{7}}{4}a^2\)