Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và mặt đáy bằng \(60^o\). Tính độ dài cạnh bên?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 4 2017
Đáp án A
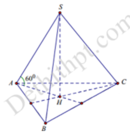
Ta có: A H = 2 3 a 2 − a 2 2 = a 3 3
S A = A H cos 60 0 = a 3 3 1 2 = 2 a 3
CM
4 tháng 12 2018
Đáp án A
Gọi H là hình chiếu của S lên lên (ABCD).
A H = 2 3 a 2 - a 2 2 = a 3 3 S H = A H tan 60 ∘ = a 3 3 . 3 = a
Thể tích khối chóp là:
V = 1 3 S A B C · S H = 1 3 · 1 2 a 2 sin 60 ° . a = a 3 . 3 12
CM
20 tháng 11 2017
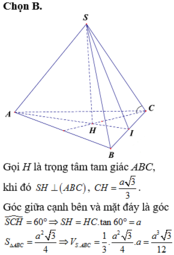
Chọn B
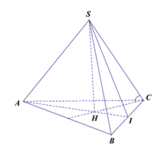
Gọi H là trọng tâm tam giác ABC, khi đó
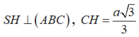
Góc giữa cạnh bên và mặt đáy là góc
CM
10 tháng 11 2018
Phương pháp:
+ Sử dụng định nghĩa để tìm góc giữa hai mặt phẳng (P) và (Q):
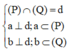khi đó góc giữa (P) và (Q) chính là góc giữa hai đường thẳng a và b.
+ Diện tích tam giác đều cạnh a được tính theo công thức S = a 2 3 4
+ Tính thể tích V = 1 3 S.h với S là diện tích đáy, h là chiều cao hình chóp.
Cách giải:
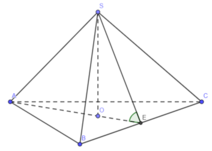
Gọi E là trung điểm của BC, O là trọng tâm tam giác ABC => SO ⊥ (ABCD) (do S.ABC là hình chóp đều)
Suy ra AE ⊥ BC (do ∆ ABC đều) và SE ⊥ BC (do ∆ SBC cân tại S)
Ta có 
nên góc giữa (ABC) và (SBC) là SEA.
Từ giả thiết suy ra SEA = 60 ° .
Tam giác ABC đều cạnh a 
Xét tam giác SOE vuông tại O (do SO ⊥ (ABC)=> SO ⊥ AE), ta có:
Diện tích tam giác đều ABC là: 
Vậy 
Chọn A
AH
Akai Haruma
Giáo viên
11 tháng 3 2021
Lời giải:
$H$ là chân đường cao của hình chóp đều nên $H$ chính là tâm đường tròn ngoại tiếp tam giác $ABC$
Kẻ $HM\perp BC$. Dễ thấy $M$ là trung điểm $BC$ và $SBC$ cân tại $S$ nên $SM\perp BC$
Do đó:
$\angle ((SBC), (ABC))=\angle (SM, HM)$
$=\widehat{SMH}=60^0$
$\frac{SH}{HM}=\tan \widehat{SMH}=\tan 60^0=\sqrt{3}$
$\Rightarrow SH=\sqrt{3}HM$
Mà: $HM=\frac{1}{3}AM=\frac{1}{3}.\sqrt{AB^2-BM^2}=\frac{1}{3}\sqrt{AB^2-(\frac{BC}{2})^2}=\frac{\sqrt{3}}{6}a$
Do đó: $SH=\sqrt{3}HM=\frac{3}{6}a=\frac{1}{2}a$
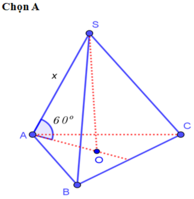
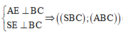
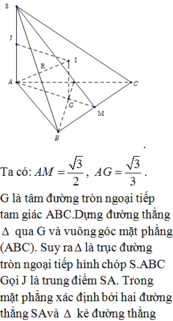
Gọi O là tâm đáy, M là trung điểm AB
Ta có: \(\left\{{}\begin{matrix}SO\perp\left(ABC\right)\\OM\perp AB\end{matrix}\right.\) \(\Rightarrow\widehat{SMO}\) hay là góc giữa mặt bên và mặt đáy
\(\Rightarrow\widehat{SMO}=60^0\) \(\Rightarrow SO=OM.tan60^0=\dfrac{1}{3}CM.tan60^0=\dfrac{1}{3}AB.\dfrac{\sqrt{3}}{2}.tan60^0=\dfrac{a}{2}\)
\(CO=\dfrac{2}{3}CM=\dfrac{2}{3}.AB\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
\(SC=\sqrt{SO^2+OC^2}=\dfrac{a\sqrt{21}}{6}\)