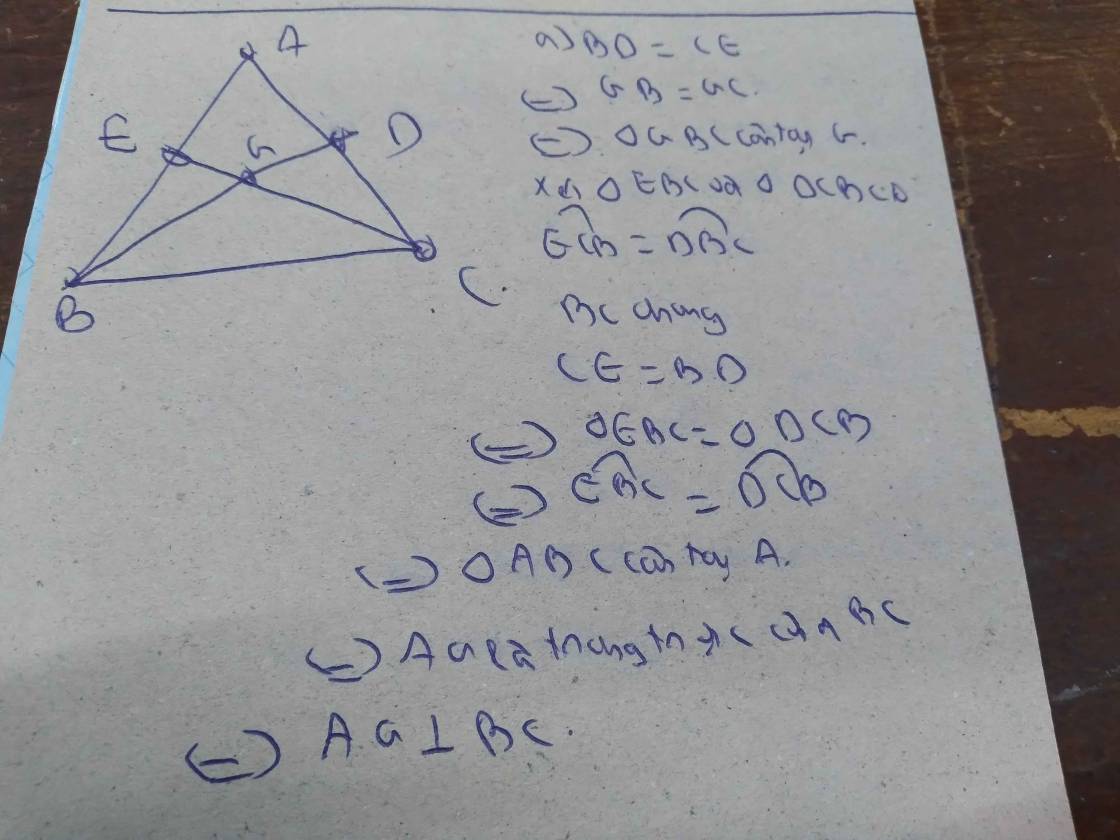
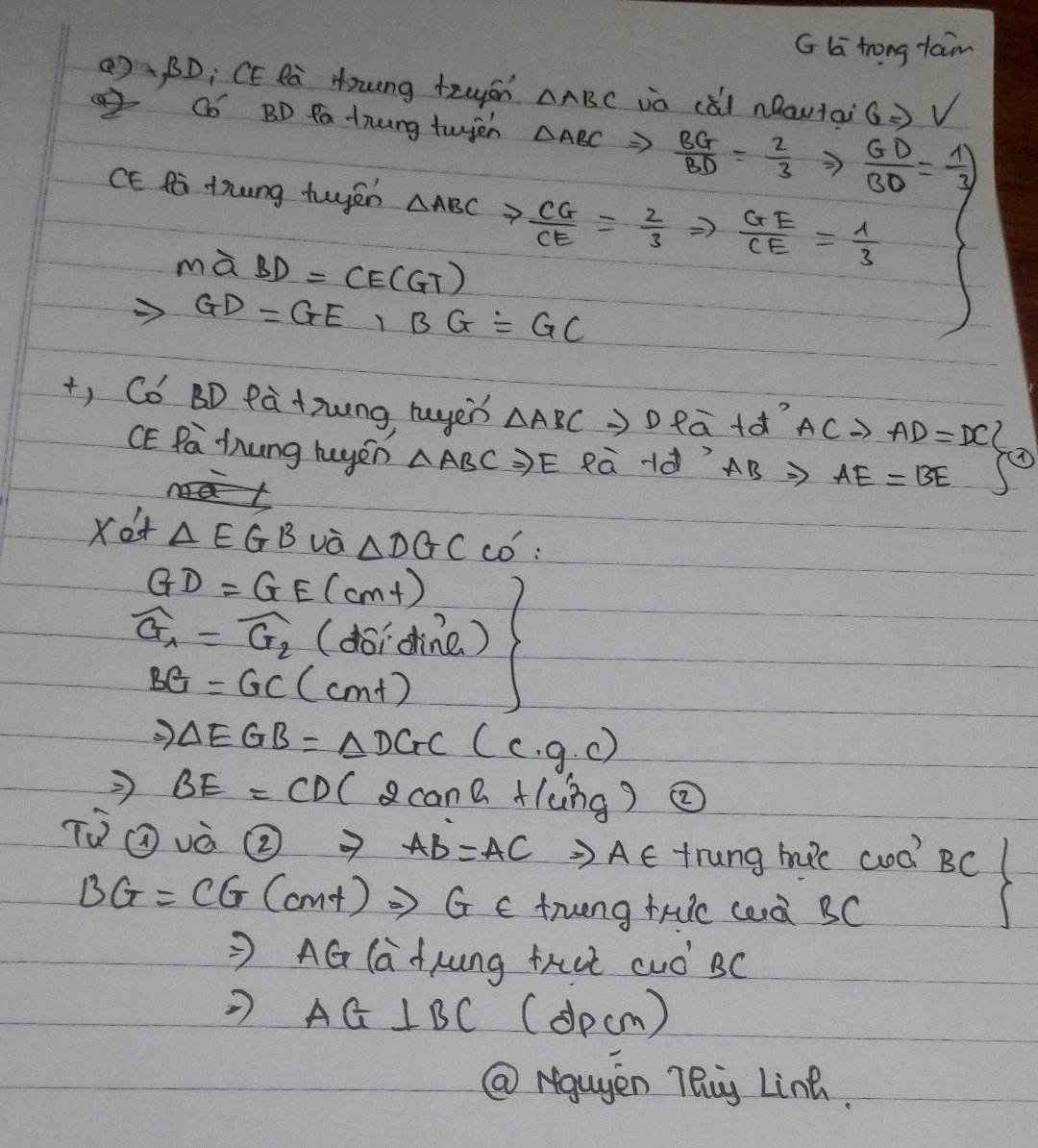cho tam giác ABC vuông cân tại A.vẽ 2 trung tuyến BD và CE cắt nhau tại G .chứng minh a)AG vuông góc với BC b)BD=CE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TK
1 tháng 5 2019
Xét tgiac ACE. ADB:
góc A chung
D=E=90¤
AB=AC
=> Tgiac ACE==ABD (c-h-g-n)
=> BD=CE ( 2ctu) và AE=AD ( sử dụng cho cậu c))
b) BD giao CE tại G=> G là trực tâm tgiac ABC
=> AG vuông góc với BC
c) Xét 2 t giác AEG=ADG ( c-h-c-g-v)
=>GE=GD(2ctu) =>GB=GC=> tgiac GBC cân tại B
28 tháng 7 2023
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
góc BAD chung
=>ΔABD=ΔACE
b: ΔABD=ΔACE
=>góc ABD=góc ACE
=>góc HBC=góc HCB
=>ΔHBC cân tại H
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
13 tháng 1 2022
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABD=ΔACE
b: Xét ΔBDC vuông tại D và ΔCEB vuông tại E có
BD=CE
BC chung
Do đó: ΔBDC=ΔCEB
Suy ra: \(\widehat{HBC}=\widehat{HCB}\)
hay ΔHBC cân tại H
c: Xét ΔABC có
AE/AB=AD/AC
Do đó: DE//BC
S
4 tháng 3 2023
xét ΔECB và ΔDBC, ta có :
EC = BD (gt)
\(\widehat{B}=\widehat{C}\) (2 góc đáy của ΔABC cân tại A)
BC là cạnh chung
=> ΔECB = ΔDBC (c.g.c)
=> \(\widehat{GBC}=\widehat{GCB}\) (2 góc tương ứng)
vì ΔGBC có \(\widehat{GBC}=\widehat{GCB}\) nên ⇒ ΔGBC là một tam giác cân (cân tại G)
18 tháng 3 2023
a: Xet ΔABC có
BD,CE là trung tuyến
BD cắt CE tại G
=>G là trọng tâm
=>AG là trung tuyên của ΔABC
mà ΔABC cân tại A
nên AG là phân giác của góc BAC
b ΔACB cân tại A
mà AG là trung tuyến
nên AG là trung trực của BC
=>GB=GC
c: Xét ΔGAC có
CK,AI,GD là trung tuyến
=>CK,AI,GD đồng quy
=>CD,AI,BD đồng quy