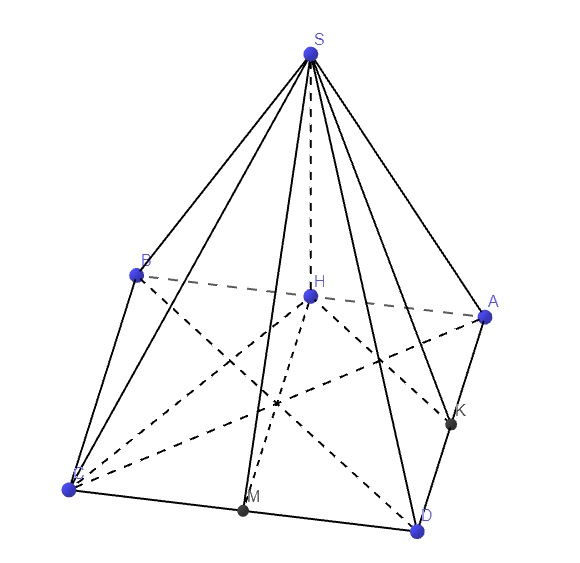
cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh AB=2a, SI vuông góc ( ABCD) vs I là trung điểm canh AB và SI=a√5. Gọi M là trung điểm của BC. a) CM BC vuông góc (SAB) và IM vuông góc (SBD) b) tính góc giữa SC và (ABCD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D.
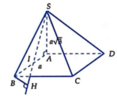
Ta có
B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ ( S A B ) ⇒ B C ⊥ S I
Gọi H là hình chiếu của B lên SI ⇒ B H ⊥ S I B H ⊥ B C ⇒ B H = d ( B C ; S I )
⇒ Δ B H I ∽ Δ S A I ⇒ B H S A = B I S I ⇒ B H = S A . B I S I = a 3 . a 2 a = a 3 2

a: (SAB) vuông góc (ABCD)
(SAB) giao (ABCD)=AB
SI vuông góc AB
=>SI vuông góc (ABCD)
b: CD vuông góc SI
CD vuông góc IK
=>CD vuông góc (SIK)
=>(SCD) vuông góc (SIK)

Trong mp(SAD) kẻ DF//SA
SA⊥AD => DF⊥AD mà AD⊥DC => AD⊥(DCF)
Kẻ CH⊥DF => CH⊥AD => CH⊥(SAD)
=> H là hình chiếu của C lên (SAD)
=> \(\widehat{\left(SC,\left(SAD\right)\right)}=\widehat{\left(SC,SH\right)}=\widehat{CSH}\)
ΔCFD=ΔSAB => ΔCFD đều cạnh a => CH= \(\dfrac{\sqrt{3}}{2}a\)
SC= \(\sqrt{2}a\)
Xét tam giác SCH vuông ở H ta có:
sin CSH= \(\dfrac{HC}{SC}\)=\(\dfrac{\sqrt{6}}{4}\)
=> \(\widehat{CSH}\)= arcsin\(\dfrac{\sqrt{6}}{4}\)

a.
Do tam giác SAB đều \(\Rightarrow SB=AB=a\)
Trong tam giác SBC ta có:
\(SB^2+BC^2=2a^2=SC^2\)
\(\Rightarrow\Delta SBC\) vuông tại B (pitago đảo)
\(\Rightarrow BC\perp SB\)
Mà \(BC\perp AB\left(gt\right)\)
\(\Rightarrow BC\perp\left(SAB\right)\)
Do \(SH\in\left(SAB\right)\Rightarrow BC\perp SH\) (1)
Lại có SAB là tam giác đều, mà SH là đường trung tuyến (H là trung điểm AB)
\(\Rightarrow SH\) đồng thời là đường cao hay \(SH\perp AB\) (2)
(1);(2) \(\Rightarrow SH\perp\left(ABCD\right)\)
b.
\(SH\perp\left(ABCD\right)\Rightarrow\) HM là hình chiếu vuông góc của SM lên (ABCD)
\(\Rightarrow\widehat{SMH}\) là góc giữa SM và (ABCD) hay \(\alpha=\widehat{SMH}\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
\(HM=BC=a\) \(\Rightarrow tan\alpha=\dfrac{SH}{HM}=\dfrac{\sqrt{3}}{2}\)
c.
Do H là trung điểm AB, K là trung điểm AD \(\Rightarrow\) HK là đường trung bình tam giác ABD
\(\Rightarrow HK||BD\)
Mà \(BD\perp AC\) (hai đường chéo hình vuông)
\(\Rightarrow HK\perp AC\) (3)
Lại có \(SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\) (4)
(3);(4) \(\Rightarrow AC\perp\left(SHK\right)\Rightarrow AC\perp SK\)

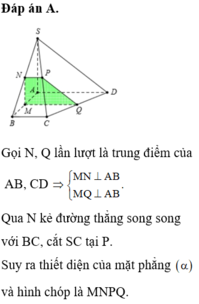
Đáp án A.
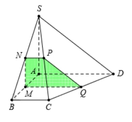
Gọi N, Q lần lượt là trung điểm của AB, CD ⇒ M N ⊥ A B M Q ⊥ A B .
Qua N kẻ đường thẳng song song với BC, cắt SC tại P.
Suy ra thiết diện của mặt phẳng α và hình chóp là MNPQ.
Vì MQ là đường trung bình của hình tháng ABCD ⇒ M Q = 3 a 2 .
MN là đường trung bình của tam giác SAB ⇒ M N = S A 2 = a .
NP là đường trung bình của tam giác SBC ⇒ N P = B C 2 = a 2 .
Vậy diện tích hình thang MNPQ là S M N P Q = M N . N P + M Q 2 = a 2 a 2 + 3 a 2 = a 2 .




giúp em vs ạ hic 😭😭