Cho hình vuông ABCD có cạnh bằng a. Gọi E;F;G;H lần lượt là trung điểm của các cạnh AB;BC;CD;DA. Gọi M là giao điểm của CE và DF. Tính diện tích tam giác MDC theo a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Phương pháp:
Sử dụng phương pháp tọa độ hóa.
Cách giải:
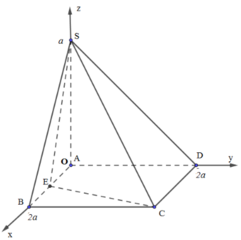
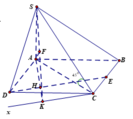
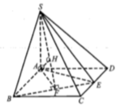
Gắn hệ trục tọa độ như hình vẽ.
Trong đó, B(2a;0;0), C(2a;2a;0), E(a;0;0), S(0;0;a)
Gọi I(x0;y0;z0) là tâm của mặt cầu ngoại tiếp hình chóp S.BEC. Khi đó, IS2 = IB2 = IC2 = IE2
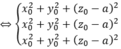
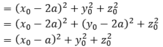
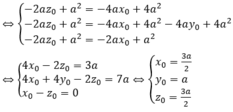
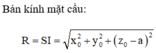
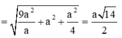
![]()


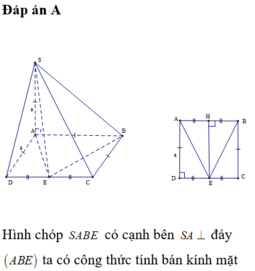
Đáp án A
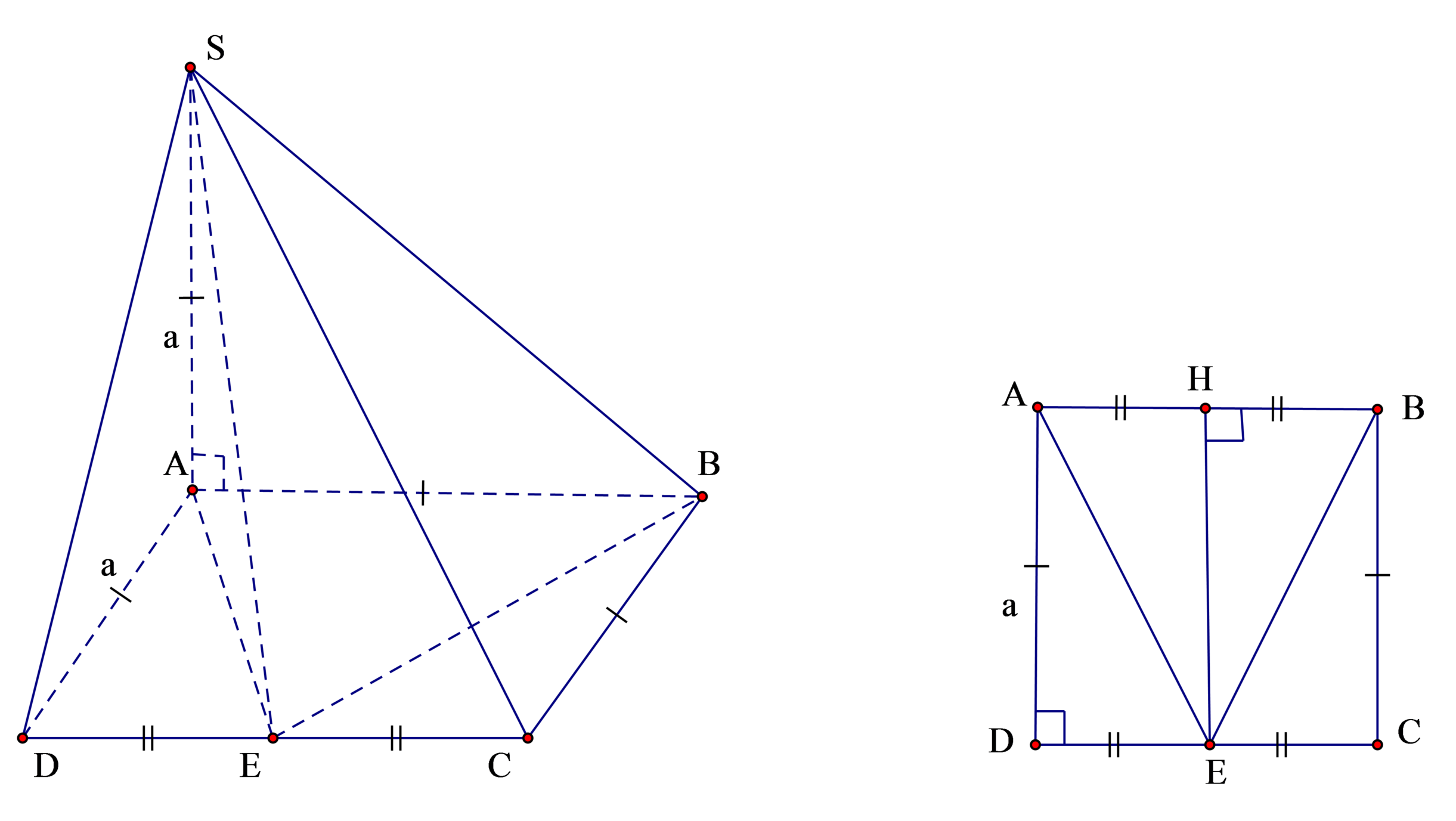
Hình chóp SABE có cạnh bên S A ⊥ đáy (ABE) ta có công thức tính bán kính mặt cầu của hình chóp dạng này là R = R d 2 + h 2 2 ( với R d là bán kính đường tròn ngoại tiếp đáy và h là chiều cao hình chóp )
Ta có: h = S A = a ; d t A B E = 1 2 E H . A B = a 2 2
A E = B E = a 2 + a 2 4 = a 5 2
R d = A B . A E . B E 4 d t A B E = a . 5 a 2 4 4. a 2 2 = a 5 8
vậy R = 25 a 64 2 + a 2 4 = a 41 8 .

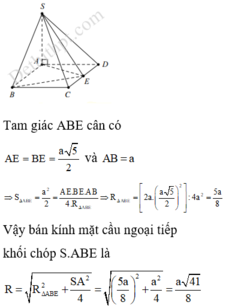
Đáp án A
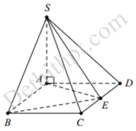
Tam giác ABE cân có A E = B E = a 5 2
và AB = a
⇒ S Δ A B E = a 2 2 = A E . B E . A B 4. R Δ A B E ⇒ R Δ A B E = 2 a . a 5 2 2 : 4 a 2 = 5 a 8
Vậy bán kính mặt cầu ngoại tiếp khối chóp S.ABE là
R = R Δ A B E 2 + S A 2 4 = 5 a 8 2 + a 2 4 = a 41 8


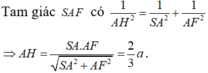


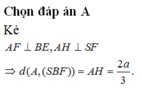
A B C D F E M
Xét tam giác vuông là tam giác BEC và tam giác DCF có CD = BC , BE = CF = 1/2a
=> Tam giác BEC = tam giác DCF (hai cạnh góc vuông)
=> góc CDF = góc BCE mà góc CDF + góc DFC = 90 độ
=> góc ECF + góc DFC = 90 độ hay góc DMC = 90 độ => CE vuông góc DF
Ta chứng minh được tam giác MDC đồng dạng tam giác CDF (g.g)
Áp dụng định lí Pytago có \(DF=\sqrt{CD^2+FC^2}=\sqrt{a^2+\frac{a^2}{4}}=\frac{a\sqrt{5}}{2}\)
\(S_{CDF}=\frac{1}{2}CD.CF=\frac{1}{2}a.\left(\frac{a}{2}\right)=\frac{a^2}{4}\)
Suy ra \(\frac{S_{MDC}}{S_{CDF}}=\left(\frac{CD}{DF}\right)^2=\left(\frac{a}{\frac{a\sqrt{5}}{2}}\right)^2=\left(\frac{2}{\sqrt{5}}\right)^2=\frac{4}{5}\)
\(\Rightarrow S_{MDC}=\frac{4}{5}S_{CDF}=\frac{4}{5}.\frac{a^2}{4}=\frac{a^2}{5}\)
chiu
tk nhe
xin do
bye